DxOMark Camera Sensor

This essay is a successor to a previous article [1] published on Luminous Landscape in early 2011.
This update explains industry trends using over 50 new camera models, discusses the impact of sensor
size and provides sample photos to illustrate some of the geekier stuff.

Introduction

DxOMark Camera Sensor is a raw benchmark for camera bodies by DxO Labs. The benchmark is “raw” because it measures image quality using Raw output files. It is also raw as DxO’s data can be used to cook up camera reviews that cover more aspects than image quality.

If you only want to compare a few specific cameras, the original data on DxOMark’s website should be perfectly adequate – although I still suggest browsing all the pictures in this article. However, if you want a deeper understanding of what the DxOMark scores really mean, if you care about tradeoffs in camera design or are wondering about major industry trends like “mirrorless” and small high quality cameras, this article might be of some use.

This article hopes to bridge the gap between scientific publications about camera sensor design (which are quite inaccessible for photographers) and consumer-oriented camera reviews. I have tried to maintain some degree of readability by including lots of diagrams, by mentioning examples, by moving details to endnotes and by adding some actual sample photos.

Why create an update?

In the 2 years since completing the previous article, the number of cameras tested by DxO has increased from 130 to 183. The changes are more substantial than the numbers suggest: few of the original 130 models are still in production.

Incidentally, the oldest tested camera on DxOMark.com is Canon’s EOS 1Ds (Photokina 2002). Consequently the DxOMark data happens to span 10 years of digital camera history [2].

Camera trends

The camera industry landscape is currently undergoing a next great migration: just like the migration from analog to digital, an increasing number of users are starting to upgrade to cameras with smaller sensors because this results in smaller and thus more convenient camera sizes.

In other words, you can get “yesterday’s” full-frame sensor quality using a modern APS-C size sensor[3]. Alternatively, you can get yesterday’s APS-C sensor performance using the best available CX format sensor[4]. In fact, you can probably match or even exceed today’s entry-level medium-format image quality with a modern full-frame sensor (e.g. the Nikon D800E).

This is not just the standard story of electronics getting a bit cheaper or better every year. It is largely due to a jump in sensor performance in the past 2 or 3 years (largely thanks to Sony sensors). It also coincides with competition on the camera market from mobile phones. This causes traditional camera makers to focus on image quality: unless your camera is a lot better than a multi-purpose smartphone, how can you convince smartphone users to carry around an extra camera when their smartphone is always at hand?

Nowadays smartphones are adequate as everyday cameras, and integrate well with popular online social services like Flickr and Facebook. Smartphone sales are thus eating into the compact camera market, prompting camera manufacturers to introduce premium compact cameras (e.g. the mirrorless Sony NEX series) that clearly outperform smartphones. These premium compacts provide near-SLR image quality while looking less intimidating. And they actually fit into coat pockets. New DSLR models, in response, increasingly target professionals and those with significant investments in DSLR lenses. As a next step in this migration, the low-end medium format cameras are under attack by high-end SLRs (e.g. the 36 MPixel Nikon D800E) because these are more versatile and have comparable image quality at lower cost.

So this migration is driven by consumers who buy the most convenient (=smallest) camera that meets their needs. While others who in the past might have upgraded to a physically larger camera format may now choose to stick to the same sensor size. This story about sensor size and sensor quality is the central question of this article: how does sensor size impact image quality?

Tableau de la troupe

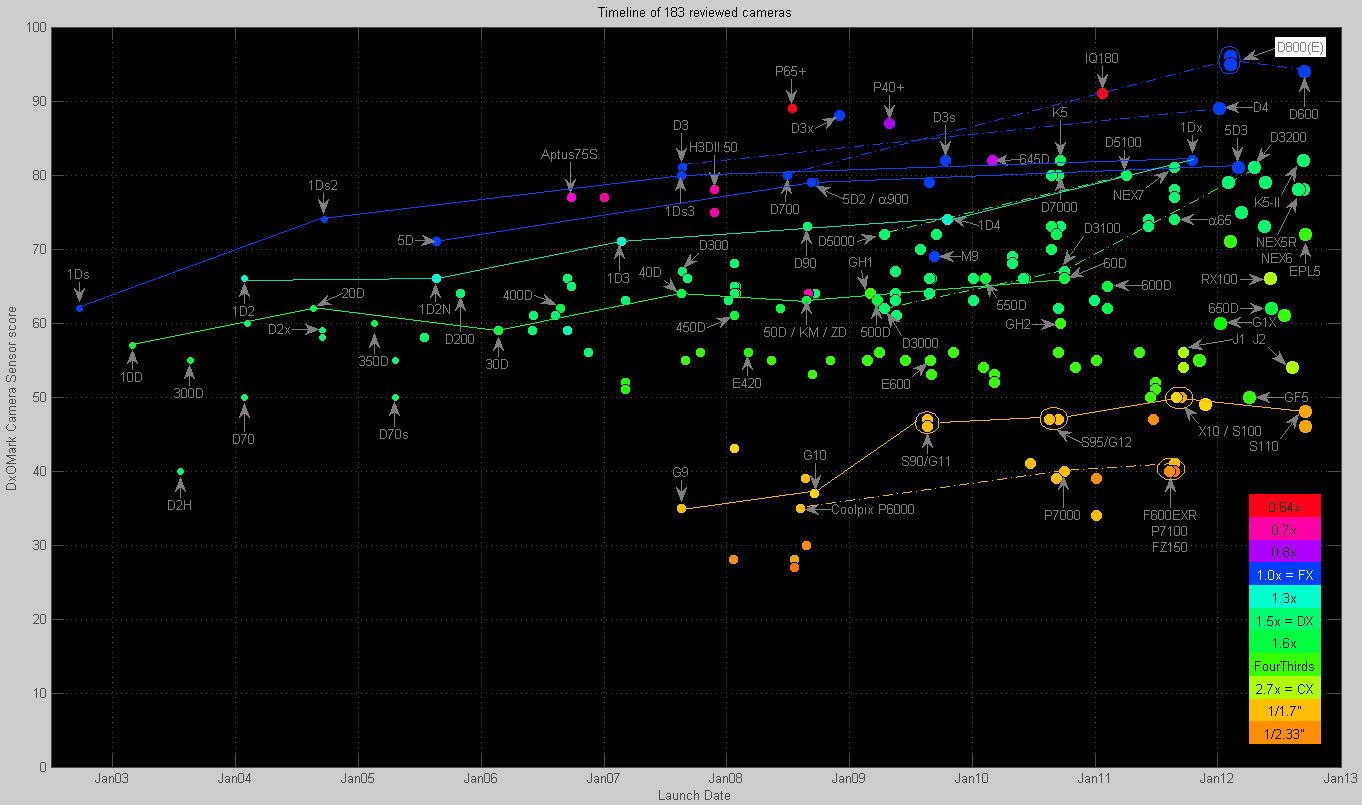
Figure 1 shows the top-level ratings for 183 cameras that have been tested by DxO Labs at the time of writing. In Figure 1, each camera is characterized with just a single number. DxOMark actually provides a total of 4 levels of info, and this single score is just the top of the information pyramid:

• A single DxOMark Camera Sensor score
• Three separate benchmarks for dynamic range, high ISO and color noise
• A bunch of graphs showing noise-related phenomena at different ISO settings.
• Multi-dimensional measurements behind tabs labeled “Full SNR” or “Full CS”.

I will mainly focus on the top two levels but occasionally reference the two other levels.

To save space, cameras in all graphs are labeled with nicknames such as “1Ds2” rather than “Canon EOS 1Ds Mark II” (1994). None of their friends call them by their full name anyway.

The data is shown for the majority of point-and-shoot cameras or camera phones.This is because the DxOMark test procedure requires that a camera can generate Raw output files – such as Canon’s CR2 or Nikon’s NEF formats. This is because conversion to JPG introduces various artifacts that would influence the results, thereby obscuring the underlying differences between the cameras. DxOMark’s approach implicitly limits the scope to cameras targeted at relatively serious users. This is acceptable because typically JPG shooters are unlikely to worry about squeezing the maximum image quality out of their camera anyway.

Figure 1 shows the overall DxOMark Camera Sensor score for each measured camera. This is the number summarizing DxOMark’s measurement data into a single figure of merit. High scores indicate a mix of low noise and high dynamic range. The two concepts are closely related, but not quite identical. A difference of 15 points in the DxOMark Camera Sensor score is a worthwhile improvement: it corresponds to a “stop”, an “EV” or a factor of 2 difference in ISO settings. Differences of 5 points (or less) are hardly visible but can be measured in a lab.

The horizontal axis in Figure 1 shows when each camera was announced. Newer models are shown in all graphs using larger dots than older models. This makes newer models stand out better in some of the graphs.

If you cannot find a major recent camera model, it means that it hadn’t been tested when I finalized this article. DxOMark gets flack on some forums for not having tests available shortly after models are in the shops. This is probably partly related to their business model, but I also suspect that manufacturers are more helpful at providing test cameras which they believe will get high scores (the manufacturers can help by supplying a production model for testing, and probably have the privilege to check benchmark results for errors before publication).

Figure 1. DxOMark scores for digital camera models launched in the past 10 years.

Click on image to enlarge. The colors indicate the size of the image sensor. Click on image to view larger. 

As shown in the legend, the colors of the dots represent the physical size of the image sensor. Orange is for the smallest (25-50 mm 2 ) sensors as used in the Canon S-110 or Fujifilm X-10. So-called Four Thirds sensors (225 mm 2 ) and APS-C sensors (330-370 mm 2 ) are shown in varying hues of green. Full-frame sensors (864 mm 2 ) are shown in blue, while so-called medium format sensors are shown in colors ranging from purple via magenta to red (2200 mm 2 ). The color scale consists of a total of 64 color steps, so intermediate sensor sizes actually map to intermediate colors.

Current sensors span a range of roughly 10× in terms of linear size and 100× in terms of area. As we shall see, sensor size in cameras plays an important role in camera performance. Analogously, a 100× range in combustion engine displacement takes you from a noisy little lawn mower engine (25 cm 3 ) to a deafening 2.4 liter Formula 1 engine [5].

Trends in the DxOMark Sensor score

Figure 1 already illustrates three key trends:

Larger sensors typically score better than smaller sensors. This is why orange dots score low (e.g. Fujifilm’s X-10), green ones score in the middle ground (numerous APS-C models), and blue/purple/red dots tend to be at the top (e.g. Phase One’s IQ-180). We will explain why later.

Newer sensor designs of any particular size (= same color dot) tend to outperform older designs with the same size. This is why the color bands are tilted: new models generally outperform older models. This trend can’t continue indefinitely due to physical limitations, but the rate of innovation in the past few years was actually higher than it used to be: the marketing guys have figured out where they want to go and the engineers knew how to get them there.

There are other factors influencing sensor performance. These can be subtle differences between a company’s level of technical expertise, its R&D budget, its patent portfolio or its market strategy. Thus a smaller sensor (e.g. the 1.5× Sony NEX-7, August 2011) sometimes actually matches a larger and newer sensor (e.g. the newer Canon 5D Mark III, March 2012) – thus masking both previous trends. In general, these are temporary anomalies because, in the end, the laws of physics and marketing will prevail.

The lines are shown in Figure 1 connect some models to their direct successors. Example: one line connects the Canon EOS 10D, via the 20D, 30D, 40D and 50D to the 60D.

Note that Nikon (dot-dashed lines) has in the past years overtaken Canon (solid lines) for many sensor sizes as far as low ISO sensor performance is concerned [6]. Some industry analysts are expecting Canon to catch up when it gets its new 0.18 µm sensor chip fabrication line operational [7].

If you take the time to study Figure 1 in a Sherlock Holmesian pensive mood [8], you will discover that the resolution of a sensor is not shown. Resolution is often interpreted as an image quality indicator by the general public but has no direct impact on the DxOMark Camera Sensor score. DxOMark Camera Sensor benchmarks the aspects of image quality that are complementary to resolution. We will come back to this.

DxOMark Camera Sensor scope and purpose

DxOMark Camera Sensor ratings essentially measure image noise and dynamic range. Despite the benchmark’s name, it covers more than just the sensor. It covers the imaging pipeline starting at the point where the light enters the camera body up to the recorded Raw file [9].

Benchmark data such as DxOMark Camera Sensor help people decide what to buy or whether to upgrade. But major benchmarks also indirectly influence industry direction. This is analogous to automotive mileage or crash tests: even if no single test is perfect, vendors will try to optimize their designs to score well on major tests.

Although DxO Labs [10] is a commercial organization, it provides this benchmark data for free because DxO measures this data anyway for their DxO Optics Pro raw converter. And providing the data helps DxO get visibility in the photography market. DxOMark’s measurement data and graphs are incidentally not in the public domain, but can be redistributed under certain conditions [11].

Noise versus Resolution

Another reason why the term “Sensor” in the name of the benchmark can be a bit confusing is that the benchmark only covers the noise performance of the camera sensor. In reality, perceived image quality is a mix of two factors that are both impacted by the sensor:

• image sharpness: is there enough resolution and contrast to render required details?
• image noise: does noise obscure details under dimly lit conditions or in dark shadows?

Engineers like to keep both separate because they are different phenomena within their formulas: in an analogy with an audio system, image sharpness corresponds to bandwidth (which frequencies can be reproduced) and noise to the hiss in an audio system.

Image noise is primarily determined by the camera body and its sensor. Image sharpness is nowadays mainly determined by the quality of lenses because it is relatively easy to make sensors with enough resolution to match the lens’ performance.

The DxOMark Camera Sensor benchmark covers only the image noise part, but measures this under varying lighting conditions and in various manifestations (dynamic range, luminance noise, color noise). Other camera properties such as the previously mentioned sharpness/resolution, but also factors like ease-of-use, robustness, frame rate and price are all out of scope.

Note that DxO Labs also publishes a second free benchmark called DxOMark Camera Lens [12] which tests camera/lens combinations. This metric mainly [13] covers the resolution resulting from the lens, the sensor, and any other optical component. So to get a full picture of the image quality of a camera/lens combination, you can use both DxO benchmarks [14].

In this article, we ignore the impact of sensor resolution on image quality. DxO itself suggests that you first decide how many MPixels you need for your purposes (e.g. Will you only view images on the screen? How much will you crop? Will you make extremely large prints?). Any camera with enough resolution should have the comparable sharpness and can then be compared using just the DxOMark Camera Sensor score. After all, there is no direct benefit in having more resolution than you will use. But as we will see, there are no fundamental drawbacks either to having surplus resolution – despite a popular misconception that high resolution results in extra noise.

Another way to look at the relevance of resolution: nowadays, unless you use expensive lenses on a relatively cheap camera, cameras tend to have enough resolution to handle what the lenses can project onto the sensor. And for most uses, 12-18 MPixels is more than enough anyway. So a properly designed noise benchmark can be used to predict image quality as long as you keep an eye on whether you have enough resolution for your needs.

Why rehash DxOMark’s data?

The data shown here is taken (with permission) from DxOMark’s website. I created new graphs to stress specific trends. My graphs don’t replace DxOMark’s graphs and tables: their interactive graphs are better for comparing individual camera models.

This article addresses various interrelated questions:

• How to interpret the DxOMark Camera Sensor results?
• How reliable are the benchmark scores and what are their limitations?
• Why do large sensors seem to outperform smaller ones?
• Is it really impossible to get identical results with a smaller sensor?
• What can we learn about the camera industry from all this data?

During the journey, I will slip in a basic course on Image Sensor Performance for Dummies. This is good for your nerd rating because it is actually rooted in quantum physics and discrete-event statistics. But all this will be explained without the use of formulas. Instead, I will use a familiar analogy that is remarkably similar: measuring rainfall by placing measuring cups in the rain. I threw in a few Greek λetteρs to remind you that we are on the no man’s land between science, engineering, and marketing.

If all this gets to be a bit too much for your purposes, just concentrate on the graphs with actual benchmark data. Questions like “At what ISO setting do you expect a full-frame camera to produce prints with the same amount of noise as a Four Thirds camera at 100 ISO, assuming both are used at f/2.8?” will not be asked during the exam [15].

Four top-level graphs

After this somewhat abstract and lengthy introduction, let’s bring on more real benchmark data for actual cameras.

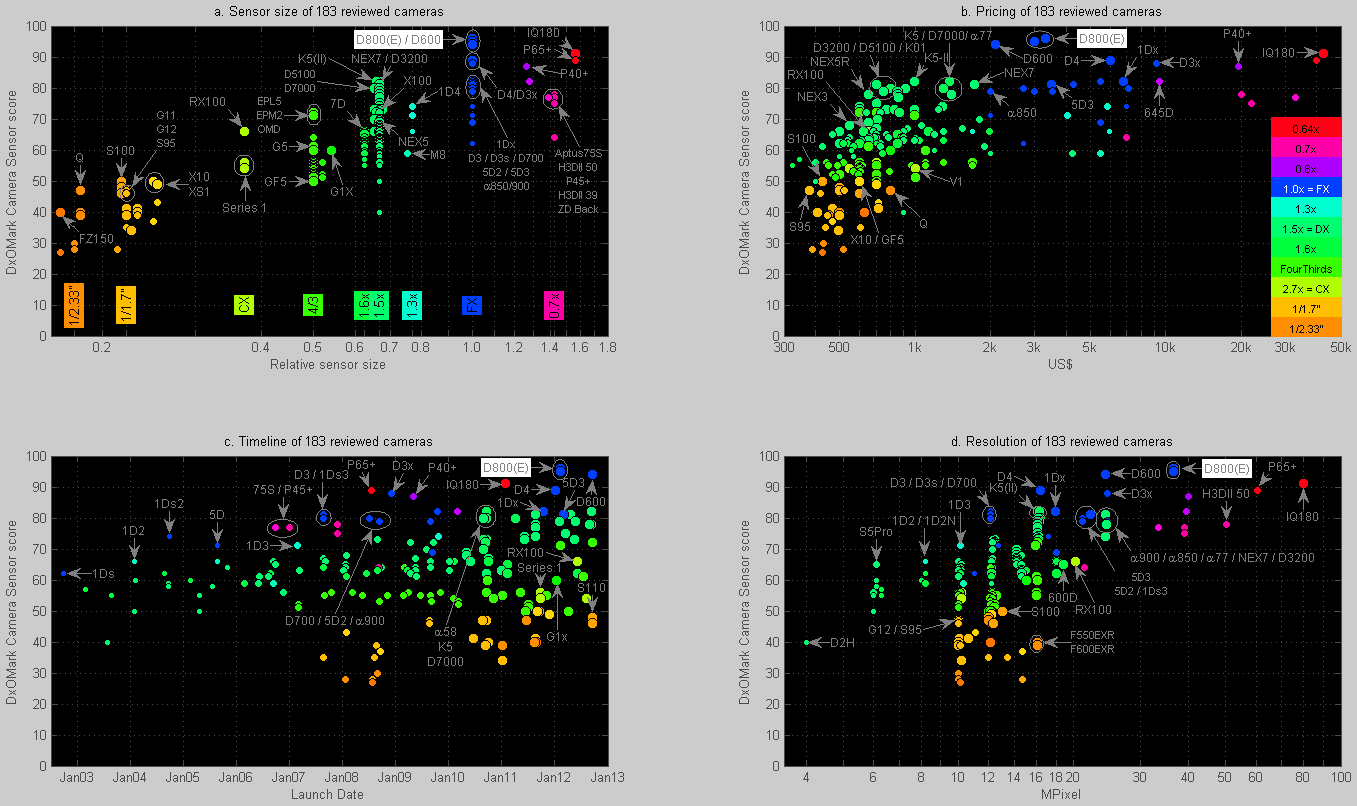
Figure 2.  DxOMark Camera Sensor score plotted against sensor size, price, launch date and MPixels.

Click on image to enlarge. The individual graphs are revisited later.

Figure 2 shows the DxOMark Camera Sensor score along all four vertical axes. The DxOMark Camera Sensor scores are currently between 27 (for an old Panasonic model with a tiny sensor) and 96 (for the Nikon D800E with its full-frame sensor). Future scores could and will likely exceed 100 at some point. The DxOMark Camera Sensor score is based on three more detailed measurements which we will discuss later (“dynamic range”, “ISO” and “color depth”). This is what I called the 2 nd level of the 4-level data pyramid. But for now, we are still at the 1 st level: a single score.

Don’t get hung up on score differences of only a few points: 5 points is roughly the smallest visible difference in actual photos (DxO says it is equivalent to 1/3 stop). The measurements themselves appear to be repeatable in DxO’s lab to within one or two points [16].

The four graphs shown in Figure 2 respectively show:

a. the impact of the sensor’s physical size on the top-level score,
b. the correlation between the overall score and the (rough) price of the camera,
c. how digital cameras have evolved over the past 10 years, and
d. how image quality is related to sensor resolution (= MPixels).

To save you some scrolling and squinting, each of these four graphs in Figure 2 will be shown enlarged when it is discussed.

Sensor size impact on image noise

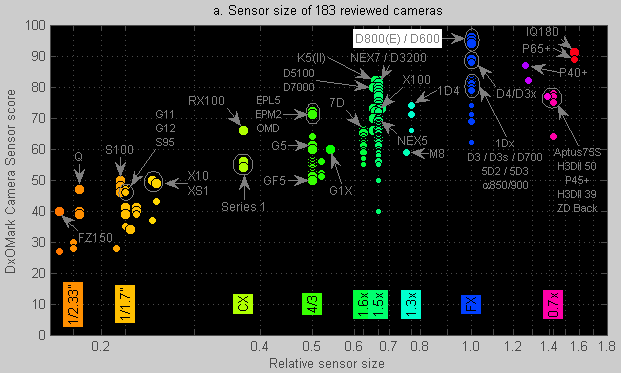
Figure 2a. DxOMark Camera Sensor scores for different sensor sizes.

This is one of the graphs shown earlier as part of Figure 2.

The horizontal axis in Figure 2a represents sensor size relative to a “full-frame” sensor (24×36 mm). A relative size of 0.5 thus means that the sensor’s diagonal is half that of a full-frame sensor and that the crop factor is 2.0× compared to a full-frame sensor. Sensors with a relative sensor size of 0.5 exist and happen to be called “Four Thirds” [17].

Figure 2a shows (from left to right):

• so-called 1/2.33” sensors used in the Panasonic Lumix FZ150 and Pentax Q (crop factor of 5.6×),
• so-called 1/1.7″ sensors (5.7×7.6 mm) also used in the Canon S110 (crop factor of 4.5×),
• so-called CX sensors with a crop factor of 2.7× as used in Nikon 1 and the Sony RX100,
• so-called Four-Thirds and Micro Four-Thirds cameras, both with a crop factor of 2.0×,
• APS-C size sensors with a crop factor of 1.5× or (Canon only) 1.6×,
• Canon’s former APS-H size sensors with their 1.3× crop factor,
• full-frame cameras (24×36 mm, with a crop factor of 1.0×), and
• medium-format cameras (crop factor of 0.8× to 0.64×).

The smaller dots represent older models and the color scale [18] represents sensor size: orange are the relatively tiny sensors, 4/3 and APS-C are shown in shades of green, cyan is mainly Canon’s 1.3x EOS 1D series, blue is for full-frame, and purple, magenta and red are “medium-format” sizes.

Figure 2a shows some interesting information:

• The best scoring cameras are the Nikon D800 and D800E twins (highlighted in white). Both are full-frame cameras (blue dots). The D800E scores 1 point higher, although that difference is negligible.
• The 1.5× APS-C market segment is very full. Especially if you include the neighboring 1.6× APS-C models by Canon.
• Some newer 1.5× APS-C products score between 78 and 82 points (just like Canon’s best full-frame models). High-scoring APS-C models currently use sensors supplied by Sony:
  • Sony Alpha-580/NEX-7/Apha-77
  • Pentax K5/K-01
  • Nikon D3200/D5100/D7000
• For APS-C sized sensors, there is no significant performance difference between SLRs, Sony’s technology with a semi-transparent fixed mirror [19] or premium mirrorless models such as the Sony NEX-7 [20].
• Except for the 1/1.7″ segment, none of the Canon models are currently best-in-class [21]. This includes the recent Canon Powershot G1X and G15, and the EOS 650D, 5D Mark III and 1Dx. Canon is lagging behind particularly in its Dynamic Range at low ISO. Canon’s competitive 1/1.7” models incidentally use Sony sensors.
• Some sensor sizes are performing well given their size while others are lagging behind:
  • Recent 1/2.33” and 1/1.7” sensors are scoring well compared to their size.
  • The Sony RX100 (CX or 1/1” format) is scoring well compared to its size.
  • The (Micro) Four Thirds format has been dormant until recently. The two new well performing models are the Olympus PEN EPL5 (72 points) and the Olympus OM-D E-M5 (71 points).
  • The 1.6× format is struggling as well, but is a Canon-only format. So it reflects the fact that Canon is currently not state-of-the-art in terms of sensor noise.
  • The 1.5x APS-C format is doing well in some models due to the use of Sony sensors and likely due to the extreme competition.
  • The full-frame format is doing very well. The five highest scoring full-frame cameras are incidentally all by Nikon.
  • Medium-format is underperforming in most (but not all) respects.

Price versus image quality

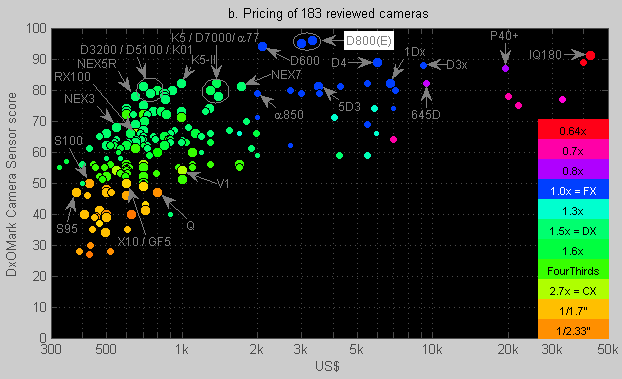
Figure 2b. DxOMark Camera Sensor scores for cameras across the price range.

In Figure 2b we can see:

• DxOMark’s database covers roughly a 100:1 price ratio ($400 – $40k).
• On a linear scale, 85% of the cameras would be squeezed into the leftmost 10% of the graph. On a logarithmic scale these 85% end up in the left half of the graph.
• Some models are old (small dots) and are no longer manufactured. Actual prices on the used market will vary from the nominal prices shown.
• Increasing your budgetcanbuy you more image quality up to around $3000. Above $3000, you may actually end up paying for high speed (e.g. Nikon D4), extreme resolution (e.g. a Phase One IQ180 digital back) or a legendary brand name (Leica).
• The Nikon D800/D800E twins (3 k$, 36 MPixels) challenge 40 MPixel medium format cameras costing 10-30 k$. The D800 twins match these medium format models w.r.t. resolution, and win w.r.t. flexibility, portability and price. According to the benchmark results, the D800(E) also wins in other image quality parameters like noise and dynamic range [22].

---

Older versus newer cameras

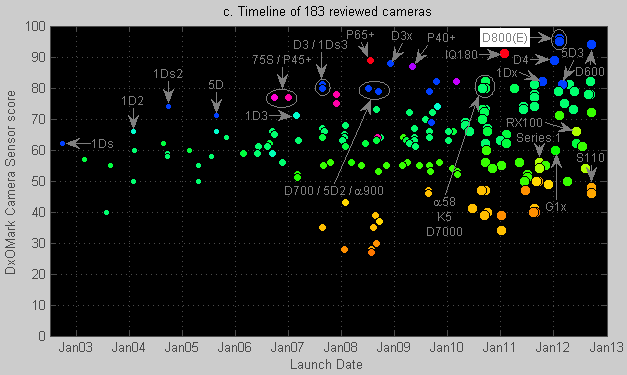
Figure 2c. For a given sensor size (color), the score tends to increase over time.

The data shown in Fig. 2c is essentially the same information shown in Figure 1, but with less annotation. 

Having too many MPixels doesn’t really help

It is important to realize that

DxOMark’s Camera Sensor score does not reward a sensor for having a high resolution.

Instead, the score is a measure for achievable print quality for typical use cases where print quality is not limited by sensor resolution. Obviously, this assumes sufficient lens quality, and that the photographer knows how to get the most out of the equipment.

So… why did DxO decide not to factor sensor resolution into the DxOMark Camera Sensor score? Firstly, this is because current sensor resolution is generally high enough for producing gallery-quality prints. Secondly, lens sharpness (rather than sensor resolution) is often the weakest link when it comes to achievable resolution. 60 line pairs per millimeter is considered an exceptionally good lens resolution. D-SLR sensors have a typical pixel pitch of 4-6 µm, corresponding to 125-90 line pairs per millimeter.

As this is important, let’s double check this by estimating what resolution is needed for high-quality prints. At 250 DPI print resolution, A4 (8.3″×11.7″) or A3 sized prints respectively require 5 and 10 MPixels. In these estimates, we assumed some white space around the actual photo. Because 250 DPI equals about 100 pixels per square millimeter, our eyes will have a tough time assessing this sharpness without a loupe. In my own experience, a  6 MPixel Canon 10D can produce great A3 prints [23] without any fancy sharpening acrobatics – providing that you used fine lenses.

These numbers are a bit surprising when you consider that sensors only measure one color per “pixel” and thus lack information compared to true pixel as defined on screens or prints (due to the Bayer mosaic [24] ). Fortunately , he camera industry is quite good at reconstructing the missing color information using fancy demosaicing [25] algorithms. It also helps that our eyes are not especially good at seeing abrupt color changes unless these coincide with sudden brightness changes. If you want to check this, the comma in the middle of this sentence is actually blue instead of black. You will probably find this hard to see against a white background. So even when viewed at “100%”, images taken with good lenses can look surprisingly sharp.

But wouldn’t we need more pixels for say A2-sized prints (15” × 20” print area)? Not necessarily: if you view bigger prints from a larger distance in order to see the image in its entirety, the required resolution doesn’t increase further and stays at the level of the (angular) resolving power of our eyes.

You will be hard-pressed to buy a new SLR camera below 16 MPixels (see Figure 3), so those extra MPixels enable you to crop your images during post-processing if needed – again assuming your lenses are top-notch. And high resolution numbers also helps impress your (male) friends at the bar or possibly the customers at your gallery.

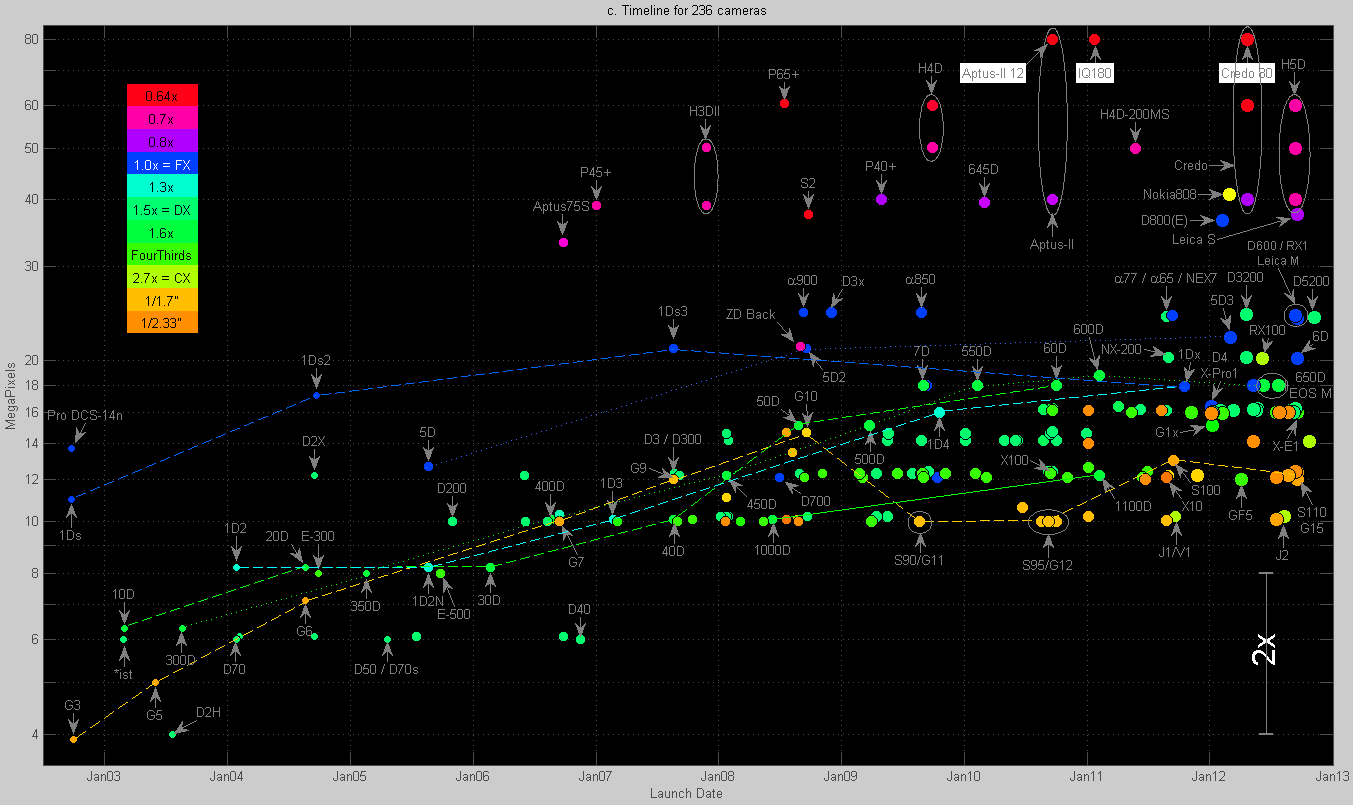
Figure 3. Launch dates versus MPixels.

Click on image to enlarge. The lines represent the various Canon product lines.

Figure 3 shows how resolution increased over the years. As indicated by the title at the top, this particular diagram shows than the 183 cameras tested by DxOMark as well as various still untested [26] cameras.

The MPixels shown along the vertical axis of Figure 3 corresponds to the general public’s measure for image quality. The rather inaccurate view that “more MPixels means higher quality” can be easily disproven by comparing Figure 2 (image quality) to Figure 3 (MPixels). For example, take the orange Canon Powershot G-series: going from the G10 to the G11, the resolution was reduced from 14.7 to 10 MPixels while image quality improved if we assume that A3-sized gallery-quality prints are more than enough for the target users.

Other highlights of Figure 3:

• The MPixel record is currently a tie between three medium format 80 MPixel digital backs. From an optics and sensor perspective there is no reason why the resolution of medium format cameras cannot be increased. The Nikon D800(E) and even the unruly Nokia 808 PureView camera phone provide the same 40 MPixel resolution as the bottom of the medium format market.
• Despite some speculation that the megapixel race might be over, and Canon’s relative restraint in recent models, current camera models typically provide 16-24 MPixel resolution, notably including the $700, 24 MPixel “entry-level” Nikon D3200.
• Canon replaced its 1D Mark IV (16 MPixel; 10 fps) and its 1Ds Mark III (21 MPixel; 5 fps) with a single model: the 1Dx (18 MPixel, 14 fps). The drop in resolution created an initial stir among 1Ds Mark III owners. The stir could have been avoided if the 1Dx had provided 21 instead of 18 MPixels, but at 14 fps the resulting data rate was apparently too hard to handle.
• Nokia’s PureView 808 is a 41 MPixel camera phone with a modest CX-like sensor size. It obviously doesn’t try to compete with a 36 MPixel Nikon D800 or a 40 MPixel Hasselblad, but uses the excess resolution of the relatively large Toshiba sensor to implement high quality digital zoom. When zooming is not required, the pixels are averaged to output 5 or 8 MPixel images with acceptable noise levels.

But having too many MPixels doesn’t harm either

More MPixels imply larger image files, thus slowing down image processing and file transfer. But the good news is that more MPixels donotincrease image noise – despite a widespread belief to the contrary.

The reason for this is that when you scale down [27] to a resolution required for displaying or printing, the resulting noise and dynamic range of the output pixels improve (assuming well behaved rescaling software). The resulting noise and dynamic range after scaling are then in theory identical to what you would have had if you had started off with a sensor with exactly the required resolution to begin with. And you may end up with a slightly sharper image as a bonus – but this is off-topic here.

Let’s look at this reasoning more closely. We will essentially discuss a bit of basic algebra – but I will leave out the actual formulas because they scare away most readers.

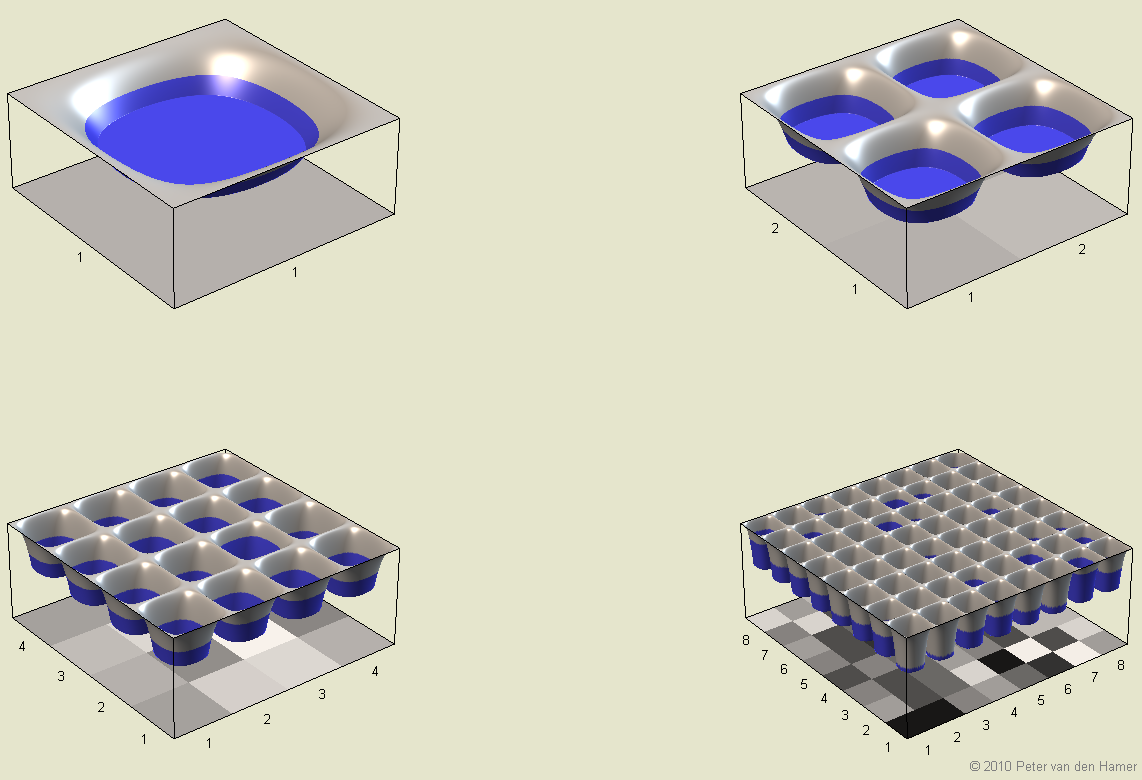
Figure 4. Impact of pixel size on noise level.

Figure 4 shows an accurate analogy to collecting photons or the basic “particles” of light: measuring the rate of rainfall by collecting rain in cups. We might decide to measure the rainfall with a single large bowl. Or, alternatively, we could use for example 4, 16 or 64 smaller cups. In all these cases the effective area used for catching drops is assumed to stay the same [28].

In the example with 64 cups, I exposed these cups to a simulated rainfall that caused each cup to geton average5 drops of rain during the exposure. For visual clarity I used really big drops (hailstones?) or – if you prefer – minute cups. However, for the signal-to-noise ratio the size of the cups doesn’t matter. Due to the statistics (Poisson distribution[29]with “λ=5”, in the jargon), on average only 17% of the cups will contain exactly 5 drops of rain after the exposure. Some cups will instead have 4 drops (17% chance) or 6 drops (15% chance), but some may contain 9 drops (4% chance) or even remain dry (0.7% chance) during the exposure to the rain.

This phenomenon explains a major source of pixel noise (“photon shot noise”[30]). This source is unavoidable and especially noticeable with small pixels, in dark shadows or at high ISO settings. The corresponding light level is shown in Figure 4 as a projected gray-scale image below the cups: empty or near-empty cups correspond to black pixels and full or almost full cups correspond to white pixels.

Now let’s look at an array of 16 (instead of 64) cups. Each cup is 4× larger and will thus, on average, catch exactly 20 drops instead of 5 drops. But, after scaling, the measurements obviously result in the same estimated rainfall [31]. Due to Poisson statistics, we may occasionally (9% chance) encounter exactly 20 drops in a cup, but we may also encounter 18 drop (8%), 21 drops (9%), or 25 drops (5%). The odds of observing 4 or 36 drops are very small but non-zero. So, although larger cups will have slightly more absolute variation when expressed in drops than smaller cups, the relative variation expressed in volume of water per surface will actually decrease as the cup size increases [32].

The point here is that proper scaling allows us to get exactly the same signal and noise levels using many small cups (pixels) or using an equivalent surface area covered with a few large cups (pixels)[33]. Thus a set of 4 cups will give you exactly the same information as a single bigger cup with a 4x larger surface area would have: just carefully pour the content of the 4 small cups into one big cup before measuring. Or weight all 4 cups together and subtract their empty weight.

Per-pixel sensor noise

Our cups-and-drops analogy gives a basic [34] model of pixel behavior.

Now let’s calculate what happens when we have plenty of light falling on a light sensor. Real pixels in a full frame 36 MPixel Nikon D800(E) with 5 μm photodiodes can hold roughly 40,000 free electrons [35] that are temporarily knocked loose within the CMOS or CCD sensor by photons. If you apply even more light, the pixel can no longer measure the difference: this is known as “saturation” to sensor experts or “burnt highlights” to photographers.

For a high-end compact camera with 2 μm photodiodes, λ drops to maybe 6,400 because of the smaller pixels. For a decent medium-format sensor, λ might reach 100,000 electrons.

A value of λ=40,000 for the Nikon D800(E) implies noise level fluctuations in the order of 200 electrons. This is because, for a Poisson distribution, the “standard deviation” equals the square-root of the expected average. A ratio of 40,000 to 200 gives a signal-to-noise ratio of 200:1 (typically 200 electron variation on an average measured value of 40,000; “46 dB” [36] in engineer-speak). This is under the best possible circumstances: it is the noise level within an image highlight at the camera’s “base” ISO setting (say 100 ISO) when you are “exposing to the right” (meaning: just before saturating the highlights).

So instead of λ=5, λ=20, λ=80 and λ=320 as simulated in Figure 4, actual sensors have “full well capacity values” or λ values of thousands or tens of thousands of electrons per pixel. The basic math, however, stays the same and tells us that if λ=40,000, the photon shot noise levels in the highlights are imperceptible to the eye[37]. For an example, see the well exposed part of Photo 1 as recorded on a Nikon D800 at 100 ISO.

Photo 1. The shadow in this 100% crop is roughly 6% gray . IMAGE MAY BE NO LONGER AVAILABLE – Link Was Removed
(100 ISO, Nikon D800, 85 mm, f/1.8)

From the Nikon D800 review at http://www.imaging-resource.com (used with permission).

Now let’s consider parts of an image that are exposed four stops lower (-4 EV, 6% gray) than the highlights. This holds for the blurred shadow in Photo 1. Each pixel here holds a signal of about 40,000/(2×2×2×2) electrons or λ=2,500. This gives a noise level of 50 electrons and a signal-to-noise ratio of 50:1 or 33 dB [38]. That level of noise is normally almost invisible, but we can see it by pixel peeping at a blurred featureless area within this 100% crop. Remember that the original image is 36 MPixel image and that we are thus seeing only 1.5% of the image. The lesson here is that even at 100 ISO, dark shadows exhibit noise that can be seen (if you deliberately go look for noise) on any camera [39].

We will now make matters worse by simulating a wedding photographer shooting with only ambient light in a dimly lit castle. Say this requires boosting the ISO from say 100 to 3200 ISO (see Photo 3). This means that we are underexposing the sensor by 32×!

Boosting ISO settings on a digital camera merely underexposes
the sensor, and cranks up the resulting image/signal by analog
amplification or by digital multiplication.

They already told you that, right?

So exposing our dark 6% gray at 3200 ISO, leaves us with an average signal level of a measly 78 electrons per pixel, with a noise level of 9 electrons – resulting in a highly visible signal-to-noise ratio of 9:1 or “19 dB”.

It is worth noting that, once you have a “full well capacity” of 40,000 electrons, the rest is just plain laws of physics. These laws cannot be changed by smart engineers or overoptimistic R&D managers. In other words, the preceding calculations tells you roughly [40] the upper limit of what any past, present or future digital camera can do.

Regardless of whether you use CCDs, CMOS, back-side illumination or even a future invention: a sensor can (and will) perform worse than these theoretical limits at high ISO – especially when the value of λ is low – due to additional noise sources within the electronics [41]. Estimates of these extra noise sources made by curve fitting data from DxOMark can be found at www.sensorgen.info.

BUT… per-pixel sensor noise is not very relevant

This gets us back to “smaller pixels give higher per-pixel noise levels”. This is a fact and we showed you how the math for this works. But, fortunately for us users, per-sensor-pixel noise is the wrong metric for prints [42]. Printing implies scaling to a (let’s assumelower) fixed resolution of (arbitrarily!) 8 MPixels. If the scaling is done well, it exactly cancels out the extra per-pixel noise which you got by starting out with more than the required 8 million MPixels.

So the following four scenarios for reducing image resolution give you the same signal levels and the same noise levels – at least according to our simplified model:

1. You can start off with an 8 MPixel sensor (“low resolution”) with the same total light-sensitive area as the other scenarios.
2. You can use a 32 MPixel sensor, but combine each 4 analog quantities before going digital. This is like pouring 4 small cups into a bowl before weighing (“analog binning”).
3. You can using a 32 MPixel sensor, measuring the output per pixel and then scaling the resulting image to 8 MPixel digitally (“digital binning” [43]).
4. You can use a 32 MPixel sensor, capturing all the measurement data in a file, and letting a PC scale the image to 8 MPixel.

Here is another example: a 60 MPixel sensor in a Phase One P65+ camera back should [44]give the same print quality and the same DxOMark Camera Sensor score as:

• a hypothetical 15 MPixel sensor with the same physical sensor size
• an image that is downscaled within the camera to 15 MPixels
• an image that is downscaled within a PC or Mac to 15 MPixels

By coincidence (as I later heard from a DxO expert) DxOMark has actually tested the second scenario for the P65+ digital back: in its “Sensor+” [45] mode with 15 MPixel output, it gets the same DxOMark Camera Sensor score as in its 60 MPixel native mode. This is reassuring for the validity of the scaling formulas.

I incidentally believe that a similar conclusion holds when youincreaseresolution rather thandecreaseit, but that case is less relevant and harder to explain in a simple way. In essence the numbers like 8 MPixels or ratios of 4:1 are just arbitrary examples. If we had explained all this using formulas instead of examples, the number 8 MPixel would have been a parameter that would have disappeared (“cancelled out”) in the final result.

Resolution and DxOMark Camera Sensor score

To summarize, the DxOMark Camera Sensor score is “normalized” to compensate for differences in sensor resolution. In other words, the DxOMark Camera Sensor benchmark doesn’t “punish” high-resolution sensors for having lots of small pixels that are individually relatively noisy. And similarly, the benchmark doesn’t favor using large pixels despite their lower per-pixel noise. This isnotsome kind of ideology or marketing manager’s claim: it is just the result of calculating how the noise level of different input resolutions would result in noise after scaling to a single output resolution.

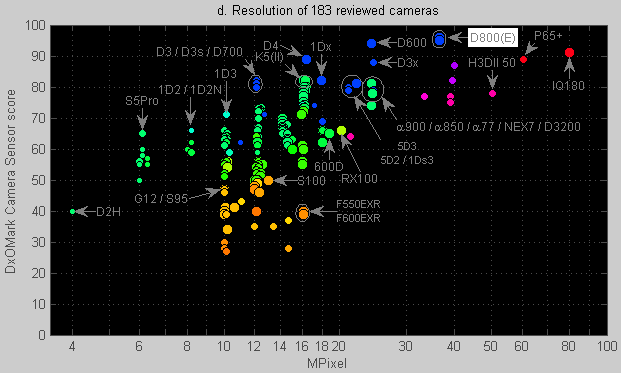
Figure 2d. Relationship between resolution and the DxOMark score.

Although high resolution does not directly increase the DxOMark score,
there is an indirect correlation because big sensors tend to have more MPixels than little sensors.

Having said all that, let’s go back to the benchmark data in Figure 2d. Despite theory explaining why squeezing more MPixels into the same sensor areashouldn’timpact image-level noise, Figure 2d seems to suggest that higher-resolution sensors actually have better performance than lower resolution sensors. This doesn’t support the myth that “increased resolution increases noise”: it in fact shows increased resolution providing decreased noise (=higher scores).

This is firstly because high resolution sensors might be bigger than lower resolution sensors, and bigger sensors have less noise. It is also because lower resolution sensors tend to be older, and sensor performance has increased over time. There is little interest in low resolution sensors, especially now that you can get high resolution sensors without a noise- or price penalty.

Question: But what about the 16 MPixel D4 that is outperformed by the 36 MPixel D800(E). These were both developed by Nikon simultaneously (launched within one month of each other) and have the same sensor size.

Answer: Again, this is no evidence supporting the “high resolution gives high noise” myth. In fact, it would support a “high resolution gives low noise” myth! In this particular case the sensors are manufactured [46] by different factories and are thus not entirely comparable.

Question: If high-resolution has no drawbacks, why not produce 50 MPixel APS-C or “4/3” sensors?

Answer: The pixel pitch would drop down to about 2.75 µm or below. At that resolution, lenses are generally the bottleneck [47] – so you won’t see much improvement in actual system resolution. Furthermore, at some point, pixels become so small that the assumed idealized scaling (with an assumed constant fill factor and constant “quantum” efficiency) will no longer apply: four 2.5×2.5 µm pixels together would capture less light than one 5×5 µm pixel (because of wiring that gets in the way, mechanical overlay tolerances on filters, “fill factor”, etc). The resulting decrease in signal-to-noise ratio would negatively impact the DxOMark Camera Sensor score.

Bigger lenses for bigger sensors? (optional reading)

To summarize: larger sensors (rather than larger pixels) have less image noise. This is because a larger sensor area can capture more light – more or less regardless of the number of MPixels the chip’s surface has been divided into.

But in order to capture more light using a larger sensor, you need a physically larger lens to capture more light to maintain the same exposure setting [48]. Here is a quantitative example:

1. Let’s compare a 105 mm f/2.8 lens on a full-frame camera to a fancy medium-format camera with a sensor that has twice the area of a full-frame sensor. Certain Hasselblad cameras have a crop factor of 0.70 (2:1 area ratio) that fits the bill nicely.
2. If we manage to mount the 105 mm lens on the medium-format camera, it may not fill the larger (1.41× = √2) image circle. But assuming it did, we would capture a wider field of view – which is not a fair comparison. So we need to switch to using a 150 mm lens to compensate for the crop factor of 0.70×. This restores the original field of view. And we need to make sure the design of the 150 mm lens creates a sufficiently large image circle.
3. If the 150 mm lens is also f/2.8, we would get the same exposure times as the 105 mm f/2.8 full-frame lens. But f/2.8 at 150 mm requires an effective diameter of the front lens that is 1.41× larger than a 105 mm f/2.8 lens. This is related to the way f-stop numbers are defined: f-stop = focal length / effective lens diameter.
4. This means that the diameter (or area) of the front lens has increased proportionally with the size (or area) of the image sensor.

This sounds credible: bigger sensors require “bigger glass” assuming that you want to use the same shutter speeds at the same ISO setting. Alternatively, you can use a 150 mm f/4 lens instead of the 150 mm f/2.8 lens. Either you underexpose your image 2×, and thus end up with no noise level improvement over the original full-frame sensor.

Finer points about sensor scaling (optional reading)

Note that, in the previous section, we decreased the depth of field when switching from 105 mm f/2.8 to 150 mm f/2.8. This is consistent with convention wisdom that “larger sensors have smaller depth of field”.

But this only applies if there is a good reason to stick to f/2.8. In February 2012, Falk Lumo argued that, for example, a 105 mm f/2.8 lens should be compared or considered “equivalent” to a 150 mm f/4 lens on a 1.4x larger sensor. This may sound odd, but keep in mind that we tend to consider the 105 mm lens equivalent to a 150 mm on the larger format as they give the same image. So it wouldn’t make sense to automatically assume that setting all numbers the same across sensor sizes automatically gives you a fair comparison.

So, in his white paper [49], Falk addresses the question whether it is feasible to make images taken with two cameras with different sensor sizes look indistinguishable. He calls this “camera equivalence”. In other words, Falk’s reasoning implies that the old wisdom that “larger sensors produce images with smaller depth of field (DoF)” and the newer digital wisdom that “larger sensors have better noise performance” are both an artifact of not comparing equivalent cameras.

So, to keep the DoF in our example equivalent you would need to use a 150 mm lens at f/4. But this in turn increases the exposure time by 2x compared to using a 150 mm lens at f/2.8. So Falk’s approach implies doubling the ISO value to essentially underexpose the image (while correcting during in-camera image processing). This in turn cancels out the noise benefit of having a large sensor. This obviously won’t make the large sensor owner happy, but does meet Falk’s goal of comparing equivalent cases. Once you reached that plateau of enlightenment, you can then presumably understand the subtle engineering tradeoffs which make one camera size fundamentally more attractive than another.

Table1. Five theoretically indistinguishable camera configurations

“Smartphone”

“Compact”

Four Thirds

Full Frame

“Large sensor”

Relative crop  factor

8×

4×

2×

1×

0.5×

Relative sensor size

0.015×

0.06×

0.25×

1×

4×

MPixels

25 MPixels

Pixel pitch

0.75 μm

1.5 μm

3 μm

6 μm

12 μm

Focal length

12.5 mm

25 mm

50 mm

100 mm

200 mm

Angle of view

23.4°

Aperture

f/0.5

f/1.0

f/2.0

f/4.0

f/8.0

Aperture diameter

25 mm

25 mm

25 mm

25 mm

25 mm

Sensitivity

1.5 ISO

6 ISO

25 ISO

100 ISO

400 ISO

Full-well capacity

40,000 electrons

40,000 electrons

40,000 electrons

40,000 electrons

40,000 electrons

Let’s test the implications of this theory by simply applying it across a 16× range of sensor sizes. We arbitrarily chose a light telephoto lens and a 25 MPixel camera [50]. This gives us the above table of cameras that would produce images that should be indistinguishable – even in a forensic lab (no wisecracks about EXIF fields please – we are doing high science here kids!). The red numbers are values that are impractical or impossible to design.

One conclusion is that we could take a workable smaller reference camera and easily produce the same results on a camera with a larger sensor. But this “emulation” comes at a cost: we may be using a f/4 lens at f/8 just to get the same depth of field. And we would be using only 25% of the 160 k-electron full-well capacity (by operating at 400 ISO instead of the native 100 ISO) just to keep the shutter speed the same. So we are essentially either under-utilizing a fancy larger sensor camera or assuming a less technology challenging larger sensor camera.

Using a smaller sensor has the opposite problem: it demands a lens on the small camera that is unrealistically fast. And it assumes we have the technology to achieve unchanged full-well capacities within smaller pixels. If we did have that technology, we could presumably have made the full-frame camera perform better.

So all this confirms in a roundabout way that large sensors can outperform small sensors or can alternatively match them using more straightforward technology.

Falk Lumo’s equivalence criterion shows you with scientific rigor that you might spend more on a larger camera without achieving any visible benefits whatsoever. But if you maintain f-stop values with increasing sensor size (and accept or even welcome the smaller DoF) you can conceivably get better image quality using a larger sensor.

The 2nd level of DxOMark scores

Let’s get back to business again. In the next sections, we examine how the overall DxOMark Camera Sensor score relates to three lower-level measurements. The DxOMark Camera Sensor score is computed using (resolution-normalized) metrics for:

• Noise levels: what is the highest ISO level that still gives a specific print quality?
• Dynamic Range: ability to record nuances in dark shadows in the presence of highlights under favorable (low ISO) lighting conditions
• Color Sensitivityor “color depth”: how much color (“chroma”) noise is there, particularly in shadows under favorable (low ISO) lighting conditions

This 2 nd level of data is measured and provided by DxOMark on their website. In fact, the DxOMark website has 4 distinct levels of information, ranging from easy to use (and thus oversimplified) to almost the raw measurements (and thus for specialists):

1. DxOMark Camera Sensor rating (one single number to rule them all). This is the number shown along the vertical axis of preceding graphs.
2. The three numbers (under the “Scores” tab) that are used to compute the DxOMark Camera Sensor rating.
3. Graphs (under “Measurements”) with e.g. the dynamic range at different ISO settings. You can use these to read out the previous level values.
4. Full noise measurements which sweep both ISO and light intensity

In the colorful graphs shown here, we stick to levels (1) and (2). But I will use levels (3) and (4) once or twice to explain strange behavior.

The 3 metrics used to compute the overall sensor ranking

These three metrics are respectively shown in Figures 5, 6 and 7. As a DxO manager, Nicolas Touchard, explained during a telephone interview:

The DxOMark Camera Sensor score is under normal conditions a weighted average of noise, dynamic range and color sensitivity information. But some non-linearities are deliberately included in the algorithm to avoid a clear weakness in one area from being masked by a strength in other areas.

It is worth noting that these three underlying measurements [51] are not entirely independent because they are all caused by sensor noise: Dynamic Range is the brightest recordable signal (at low ISO) divided by the background noise. Color Sensitivity or Color Depth indicates whether small color differences are masked by chroma noise. And Low-Light ISO tells you at what ISO settings on different cameras will give you equivalent noise levels.

Although a camera that is great on one noise metric will probably perform pretty well on another, different cameras do in fact win first place in each of the 3 categories. This confirms that we are not just seeing the same data represented in three different ways.

DxO at some point tried to link the metrics to different types of photography (“Use Cases”), but DxO is fortunately starting to deemphasize this as the mapping between the 3 measurements and the Use Cases was not always helpful. Here were the mappings – for what it’s worth:

Metric

Assumed lighting

DxO Use-
case name

Description

Dynamic Range

Enough light = low ISO

“Landscape”

This metric assumes that you use a tripod if needed. Many other types of photos can have a large contrast: architecture, portraits, night photography, weddings. A high Dynamic Range allows you to make large exposure corrections (if somehow your metering went wrong) or to do HDR post-processing using a single raw image.

Low-Light ISO

Challenging lighting
= high ISO

“Sport”

This metric assumes you need to go to higher ISO. This is relevant for many other types of photography: street, wildlife, news, weddings, night, concerts, and family. Most photographers need high-ISO settings regularly.

Color Depth

Enough light = low ISO

“Portrait”

This metric assumes you have enough light but may be a fair indication of what you would get in low light. Essentially it measures choma noise in the dark parts of a low-ISO image. Portraits may be less critical as chroma noise could be filtered out (at the cost of resolution) or you may be able to boost your lighting.

So all-in-all, I recommend not taking the Landscape, Sport, and Portrait naming too seriously. At best they are nicknames, and particularly “Portrait” is the least accurate of the bunch.

We will now discuss how the 183 cameras perform on each of these three metrics.

Dynamic Range at low ISO

Image Link Is Missing – and has expired (sorry)

Figure 5. For Dynamic Range, Nikon’s D800(E) and D600
are marginally ahead of Pentax and Nikon APS-C cameras

DxOMark’s definition for their Dynamic Range metric says:

“Dynamic Range corresponds to the ratio between the highest brightness a camera can capture [..]
and the lowest brightness [..] when noise is [as strong as the actual signal].”

So far, this is a pretty standard definition. It tells you how many aperture stops of light (EV = bit = factors of two) can be captured in a single exposure. It is analogous to asking how much water a bucket can hold, expressed in the smallest accurately measurable unit.

Elsewhere in the documentation we find that Dynamic Range (in so-called “Print” mode) is

“normalized to compensate for differences in sensor resolution.”

This scaling calculates what the dynamic range would be if you scale the image to a resolution of 8 MPixel. The choice to show the results for 8 MPixels is not really relevant unless you want to compare DxO scores to measurements from other sources: any other number of MPixels would add a constant offset (in EV) to the published Dynamic Range scores. So you can simply forget that number – you just compare DxOMark dynamic range numbers to each other and the difference between two cameras in EV is independent of the resolution of your camera or how large you choose to print the results.

Furthermore the Dynamic Range used in the overall benchmarking is themaximumDynamic Range as

“measured for the lowest available ISO setting”[typically between 50 and 200 ISO].

Today’s sensor with the highest Dynamic Range score, the Nikon D800(E), spans over 14 stops at 100 ISO. The results for the Pentax K-5II(s) and Nikon D7000 are actually very close[52]to those for the D800(E). DxOMark’s Dynamic Range plot for these cameras shows that their Dynamic Range drops by almost one 1 EV each time the ISO is doubled. This resembles an ideal amplifier that amplifies the sensor’s signal and noise without adding noise of its own. That is impressive.

Low ISO Dynamic Range and Canon

At present, Canon cameras underperform on the Dynamic Range test or, more precisely, on dynamic range measured at low ISO settings. At high ISO, the Canon 1Dx actually has abetterdynamic range than the D800(E), and the Canon 5D3 matches the D800(E) at high ISO. This confirms that newer Canon models like the 5D3 and the 1Dx are state-of-the-art as high ISO cameras.

But the problem with Canon (and all tested sensors except those with the latest and greatest Sony sensors) is that the dynamic range hardly increases when you go below about 800 ISO. This is consistent with test photos that show that the 5D3 cannot match the low ISO clean shadow performance of the D800(E), the K-5(II/IIs) or the D7000.

This is illustrated in Photo 2 that shows a 750×750 pixel crop of a 21 MPixel wedding[53]photo taken at 200 ISO on a Canon 5D Mark III. The top of the image is exposed at 100%[54], while the bottom contains 0.05% gray[55]. This implies an estimated dynamic range of 2000:1 or 11 EV. DxOMark’s more precise measurement gives 11.65 EV of dynamic range for the Canon 5D3 at the 200 ISO setting.

Note that the noise at the bottom of Photo 2 exhibits horizontal “banding”. As the camera was held in portrait mode, this is normally calledverticalbanding or “fixed-pattern column noise”. If you cannot see this (or details in the other photos) be sure you are viewing this on a calibrated monitor. And you may want to save the picture and inspect it in a trustworthy photo viewing application such as Photoshop, Lightroom or Capture One.

Sony claims[56]that they are the first and only sensor supplier so far that is able to avoid visible fixed pattern (column) noise. For this, Sony uses a combination of having on-chip analog to digital convertors (one ADC per column[57]) and a digital trick to elegantly subtract the black or empty level of each sensor pixel. In our rain & cups analogy, it is like emptying the cup before starting the measurement, first weighing it (with any residual water inside), then exposing the cup to rain, and then weighing the cup a second time. Subtracting the original weight avoids measurement errors due to the “empty” weight and due to measurement offsets. In sensor engineering, this technique is known as Correlated Double Sampling and is standard for both digital weighing[58]and for light sensors, but Sony has a somewhat cooler way to do this.

Photo 2. The shadow in this 100% crop is about 0.05% gray (-11 EV) and shows banding

(200 ISO, Canon 5D Mark III, 24 mm/1.4L II, f/2.8, 1/128 s)

Canon users frequently wonder whether Canon will catch up, particularly in terms of low ISO dynamic range – given that it has lost the lead since the Nikon D3x back in late 2008. Some industry analysts[59]expect that Canon will catch up when they start using a new state-of-the-art 0.2 μm copper[60]sensor manufacturing process which they are currently testing. This allows Canon to switch from off-chip analog to digital converters to on-chip per-column ADCs.

Final thoughts on Dynamic Range

Figure 5 shows two camera models (unrelated to the new Sony sensors) that perform unusually well given that they were respectively introduced in 2004 and 2006: the Fujifilm FinePix S3 and the S5 with Dynamic Ranges of 13.5 EV. This was achieved by combining large and small photodiodes on the same sensor. The small photodiodes can capture the highlights without overflowing, while the larger photodiodes simultaneously capture the darker parts of the image with less noise. The signals from the two sets of pixels were merged digitally into one HDR image. This technology never reached widespread introduction.

Experiment: If you want to learn more by playing with the data yourself, trying looking up (under DxOMark’s tab “Full SNR”) the gray level at which the signal-to-noise ratio drops to 0 dB for the 80 ISO curve[61]. For the Pentax K-5 II this is at a gray scale value of 0.008%. The brightest representable gray shade is 100%. So the ratio is 100/0.008 = 12500:1 which gives log(12500)/log(2) = ln(12500)/ln(2) = 13.6 stops.

But we are not finished. The “Full SNR” values in that particular DxO graph are “Screen mode” meaning not resolution-normalized. So we still need to correct for the K-5 II’s resolution of 16 MPixels rather than 8 MPixels. The noise scales with the square root of this ratio, thus giving an extra 0.5 stop[62]of Dynamic Range when scaled to 8 MPixels. The resolution normalized value for the low ISO Dynamic Range listed by DxOMark should thus be about 13.6+0.5=14.1. The actual value by DxOMark is indeed 14.1.

Apart from confirming that we kind of understand how the benchmark works, this exercise shows that a 2× difference in resolution corresponds to a mere 0.5 EV difference[63]between Screen Mode and Print Mode.

Low-Light ISO score

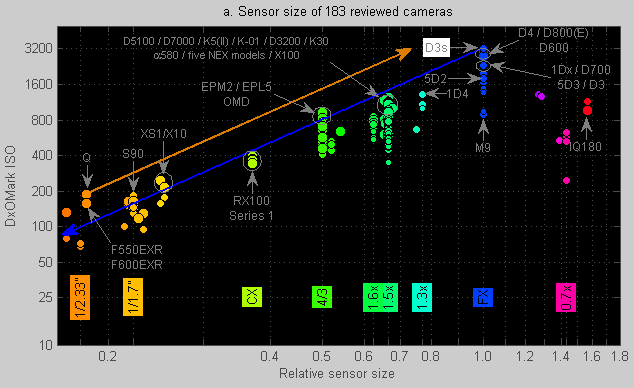
Figure 6. The cameras with the 10 highest ISO scores are all full-frame models.

Here is DxOMark’s definition for their Low-Light ISO score:

Low-Light ISO is [..] the highest ISO setting for the camera such that

• the Signal-to-Noise ratio reaches this 30dB value[32:1 ratio at 18% middle grey] 
• while keeping a good Dynamic Range of 9 EVs[512:1 ratio] 
• and a Color Depth of 18 bits[equivalent to 64×64×64 distinguishable colors].

This is a rather complex definition with built-in non-linearities: you are essentially supposed to increase [64]the ISO value until you break any of the above three rules. Due to this definition, the outcome can be anywhere in the ISO range [65]– not just values normally considered to be high ISO.

Low-Light ISO is again computed using a reference resolution.

The general idea behind this Low-Light ISO metric is simple: it tests which ISO level still gives acceptable image quality using a somewhat arbitrary criterion for exactly what “acceptable” means. As Figure 6 shows, the best camera on this particular benchmark is the 12 MPixel Nikon D3s.

Currently, the 16 highest ranking cameras on the Low-Light ISO benchmark are all full-frame sensors.
So, full-frame is clearly a good choice if you regularly work in low light conditions.

The blue scaling line in Figure 6 shows how other sensor sizes would score if they would perform as well as the Nikon D3s – but corrected with a handicap to compensate for their smaller sensor size. In other words, the blue line shows what would happen if you take the same technology of the D3s sensor and make it smaller by trimming off- or simply ignoring the edge pixels [66].

The blue line in Figure 6 shows that the best 1.5x APS-C cameras and the best CX-sized sensors are all on par with this hypothetical scaled down D3s. This is clearly not the case for medium-format sensors: these should be able to deliver “acceptable” (according to DxO’s definition) images at 6400 ISO. But actual medium format sensors perform 5-10 times worse than they should. Commercially this may not be a big deal because these SUVs of the camera world are often used on tripods or in studios with flashes. So, although there may not be a sufficient market for this, record-breaking high ISO and high dynamic range cameras should be possible with large sensors.

Another surprise is that the smallest sensors manage to outperform the blue D3s scaling line. The orange scaling line shows that the diminutive Pentax Q is currently best at high-ISO if you assign a handicap for sensor size. This doesn’t mean that the Pentax Q has very low noise. On the contrary: it needs to be operated at 200 ISO to get the same print quality as the D3s at 3200 ISO. But in view of the size handicap, various of the smaller cameras do a surprisingly good job [67].

Experiment: If you want to play with the ISO numbers, you can look up (under “Full SNR” for the Pentax K-2 II) the ISO setting at which 18% gray gives a 30 dB (5 EV) signal-to-noise ratio [68].

To get the more relevant resolution-normalized ISO value, you have to use a value of 27 dB instead of 30 dB. Those 3 dB compensate for the 2x higher resolution of the K-2 II’s 16 MPixel sensor.

Interpolation of the values for 800 and 1600 ISO gives a Low-Light ISO value of 1,353. Because the actual sensor sensitivities of cameras deviate [69] from the nominal ISO values, we can improve accuracy by using the calibration curve measured by DxOMark for the K-2 II. This gives a result of 1277 ISO, which is 0.1 stop higher than the actual DxOMark value of 1235 ISO.

Interpreting the Low-Light ISO benchmark

Photo 3 was taken at the very end of the same wedding party, again a Canon 5D3, but at 12800 ISO. You can tell how little light there was: the man’s face in the background is partly lit by the display of a cell phone that he is apparently checking.

Because the ISO settings have been boosted by 6 stops compared to Photo 2, the noise is clearly visible at this magnification. I could have suppressed the noise by filtering or using a different raw convertor. But the point of the photo is that the banding that was visible in Photo 2 is not visible at high ISO. This is because at 12800 ISO the analog signal gets amplified 64× compared to the 200 ISO in Photo 2. This amplifies both signal and noise, thereby masking fixed pattern noise or “banding” (as seen at the bottom of Photo 2) as introduced downstream in the circuitry.

Photo 3. This 100% crop shows clearly visible noise but no banding at 12800 ISO.

(12800 ISO, Canon 5D Mark III, 24 mm/1.4L II, f/1.4, 1/90 s, raw converter LR4.3RC at default settings)

The two photos thus show two distinct noise-related phenomena:

• Photo 2 shows what over 11.6 stops of dynamic range at low ISO look like: the Canon 5D Mark III (like most others) shows banding in dark shadows. This is marginally visible, but can become prominent if you apply post- processing to boost the shadows.
• Photo 3 shows what 8 stops of dynamic range look like at extremely high ISO: the same camera (like all others) shows clearly visible noise. But this time without banding.

The two phenomena are different in the same sense that an athlete may be better at running long distances while another is better at short distances. All distances involve running fast, but athletes seldom excel at both the sprint and the marathon.

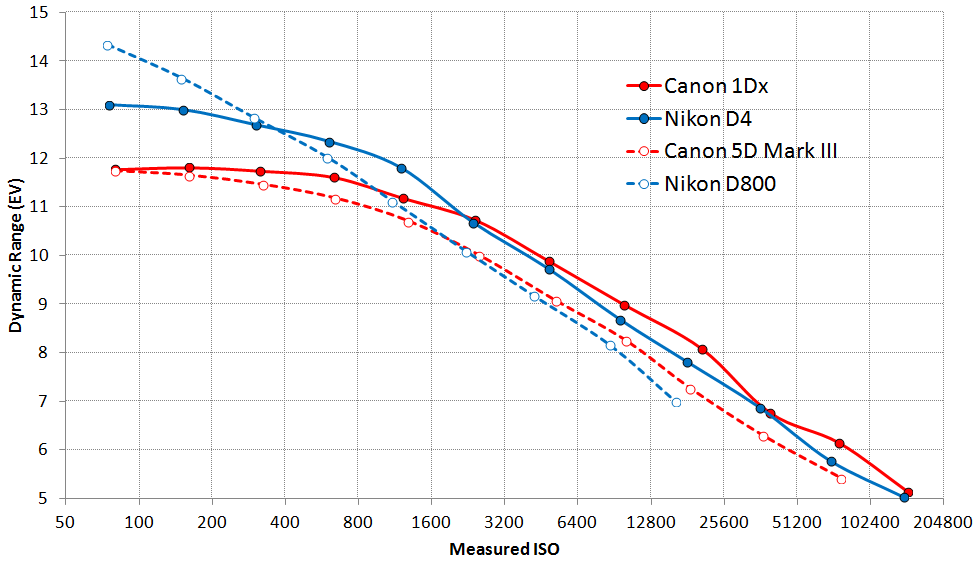
In principle, I think that a camera can be both good at high DR (at low ISO) as well as having low noise at high ISO. Figure 7 shows the DxOMark data for the top two Canon cameras and the most similar Nikon models.

Figure 7. DxOMark’s dynamic range results across a range of ISO settings.

The high overall DxOMark scores for Nikon are due to superior low ISO Dynamic Range.
But actually the equivalent Canon models have marginally better high ISO Dynamic Range.

You can find DxOMark’s Dynamic Range score by following each line to the left until it stops. The Low-Light ISO values for these models are around 3000 ISO, so can be compared by checking who is ahead in middle of the graph.

Again, the question is what we see from this graph:

1. The Nikon D4 is a better high ISO camera than the D800. Something similar holds for the Canon 1Dx compared to the 5D Mark III.
2. An ideal sensor would have a straight line as dictated by the physics/math. The Nikon D800 comes close with its excellent Sony sensor, resulting in a high low-ISO dynamic range. The Nikon D4 does not use a Sony sensor.
3. The dynamic range of both Canons saturates under 800 ISO. This corresponds to barely noise in dark shadows. This noise can be a problem if you need to render detail within those shadows.
4. At high ISO, all four models are comparable with a slight lead for the Canon models.
5. At the two highest settings, DxOMark states that the Canon 1Dx gets a minor boost by filtering away a bit of noise at the cost of detail. You could alternatively do this in post-processing.

Low-ISO Color Sensitivity

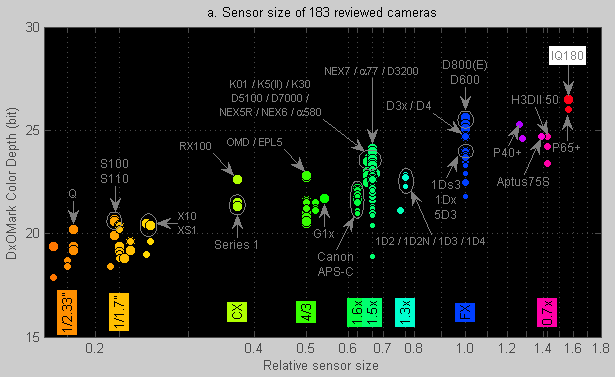
Figure 8. Color Sensitivity appears to be best in the largest sensors.

In a color sensor the green, red and blue color components are measured independently. The ratio between these values determines the perceived color. So independent noise in each channel impacts the ratios and thus impacts the apparent color.

Here is DxOMark’s definition for their Color Depth score:

Color Depth is the maximum achievable color sensitivity, expressed in bits. It indicates the number of different colors that the sensor is able to distinguish given its noise.

The metric thus looks at local color variations caused by this noise. It does not represent color accuracy – although a form of color accuracy data can be found deeply buried in the DxOMark Camera Sensor data [70].

The benchmark values for Color Depth are again normalized with respect to sensor resolution. And, again, the phrase “maximum achievable” actually means that the Color Sensitivity is measured at the lowest (e.g. 100) available ISO settings.

As shown in Figure 8, larger sensors clearly tend to have a larger Color Depth score. This is largely explainable by their lower noise at full well capacity (see Figure 4). But color noise also depends on the choice and performance of the microscopic color filters that allow the photodiodes to measure color information (not shown in Figure 4). If less saturated color filters (e.g. “pink instead of red”) were used, then the three color channels would respond only marginally differently to different colors. This would lead to a higher general/luminance sensitivity of the camera, but would introduce more color noise.

For more information on the role of the “color response” of color filter arrays, see this white paper [71] where DxO points out the impact of differences in color filter design between the Nikon D5000 and the Canon 500D [72].

A Color Depth value of 24 bit incidentally means that there is a total of 24 bits of information in the three color channels [73].

So how fair is the DxOMark Camera Sensor Score?

There is a difficult but important question. Probably every image quality scientist[74]in the world would have a somewhat different personal preference for a benchmark like this. But my impression is that the benchmark is pretty useful: I analyzed the model and the data, but didn’t find any serious flaws. Reassuringly, results like Figure 1 also appear to be pretty consistent with traditional hands-on reviews: camera models that were stronger [or weaker] than state-of-the-art at the time when they were introduced (such as the Canon 40D [or 50D]) show up as expected in Figure 1. And, as mention at the start of the article, having a pretty solid metric by an independent party is better than never-ending discussions about what the ultimate benchmark might look like.

The list of critical notes, suggestions and open issues are relatively subtle because the entire topic is a bit subtle:

Low ISO bias

If you compare the DxOMark data in Figure 7 for a number of prominent cameras you would get a more balanced impression about which camera to buy than by just looking at the overall DxOMark Sensor score. If you focus on the latter, you would strongly prefer the Nikon D800 with its excellent low ISO dynamic range. But this emphasizes one aspect of the sensor (essentially the ability to do single shot HDR) that provides a capability we never had in the past. It is a feature which we may infrequently need – and one that some types of users may never see (e.g. if you shoot JPG).

However, at sufficiently high ISO, other models win. High ISO usage may be a more relevant usage for many users than HDR ability at low ISO.

One can therefore ask whether DxOMark hasn’t overstressed low ISO noise [75]. This may explain why some reviewers arrive at different conclusions about the image quality of the Canon 5D3 (or 1Dx) compared to the Nikon D800 (or D4).

To DxOMark’s credit, the user does get three detailed scores to choose from. So you can focus on “dynamic range” if you need single-shot HDR like capability and “low light ISO” if you need to boost your ISO settings often.

Comparing different sensor sizes

As pointed out by Falk Lumo [76], the fact that larger sensors tend to have higher DxOMark scores than smaller sensors is not a guarantee that bigger is better – even if you check out the actual DxOMark Sensor scores before selecting a camera.

Say you are considering an APS-C model like the Fujifilm X-E1 versus a full frame camera. Falk Lumo’s point is that the intrinsic definition of the DxOMark metric (as well as most other benchmarks) assumes that you would compare say Fujifilm’s 35 mm f/1.4 lens to an “equivalent” 50 mm f/1.4 lens on full frame. This reduces the depth of field on full frame while decreasing the noise. But if we had kept the depth of field[77]constant (by picking a 50 mm f/2.0 lens on full frame), the noise would have stayed the same. So one can argue that the DxOMark (and any other comparison across formats at constant ISO setting) makes larger formats look good by assuming that we increase the total influx of light falling on the larger sensor by picking increasingly large diameter lenses (constant aperture).

Complexity of interpreting the numbers

Complexity is a fact-of-life in the high tech industry. To DxO’s credit, DxOMark allows you use just a single overall score to compare camera body image quality. They alternatively allow you to zoom in (and get 3 numbers instead of one) or zoom in all the way (for graphs with the actual measured data). But despite or possibly due to all this data, it is difficult to translate a conclusion of “A is 20 points better than B” into what exactly you would expect to observe in actual photos. Because I initially had trouble translating the numbers into “What type of images would this difference show up in?”, I added some photos to this essay now I believe that I more or less figured it out.

The undocumented Master Formula

DxO does not document how the final DxOMark Camera Sensor score is computed from the individual Dynamic Range, Color Sensitivity and Low-Light ISO scores. I feel it should be provided as the overall score gets a lot of attention. With the formula, DxO countered, a manufacturer could attempt to optimize the overall score. But I still don’t see benefits to leaving this formula undocumented: if DxO believes the master formula is a reasonable approximation of what photographers are looking for in a camera, they should document it with a note that it is a compromise between completeness and ease of use.

Here is my own attempt at a recipe to compute the overall score from the three subscores. Start off with the DxOMark Camera Sensor score for the Leica M8 as an arbitrary reference point. This give you 58 points. Next add 4.3 points for every extra bit of Color Depth that a camera has compared to the M8. Then add 3.4 points for every extra unit of Dynamic Range that the camera has compared to the M8. And finally add 4.4 points for every factor 2 improvement in ISO relative to the M8. The formula version seems to predict accurately to within 1 or 2 points [78].

Use case names

The Landscape/Sport/Portrait terms can easily confuse people who take this literally. I am tempted to interpret the 3 metrics as Dynamic Range (as DxO does), Luminance Noise (instead of Low-Light), and Chroma Noise (instead of Color Sensitivity). Those are quantities you find more often in reviews.

Print versus Screen mode

To compare DxOMark Camera Sensor scores between cameras with different resolutions, you need to look at the “Print” results. The overall DxOMark Camera Sensor score is “Print” level only, which is fine. For the next level of detail a viewer gets to choose between Print and Screen. This is less fine: Screen is not normally useful for end users (it can be useful for debugging your own calculations). The lowest level of data is presented in “Screen” mode only, but is not labeled as such. I would prefer to see all data to be labeled Print/Screen or –better yet– Normal/100%.Normal would stress that this is what matters. And 100% is similar to pixel peeping: here you look at the noise at the 100% crop level and loose the overview of what it means at the image level.

Why measure Color Depth at low ISO?

High-ISO chroma noise seems more relevant for photographers than low-ISO chroma noise. I doubt people are actually able to see color noise at such low ISO: it’s hard enough to spot regular noise at low ISO, and chroma noise is even more elusive. I suspect that the choice to use low-ISO Color Depth is an artifact of originally trying to define a metric that matched studio portrait conditions. But I am not convinced that a studio portrait photographer typically has problems with visible chroma noise in the first place.

Metric measurable per ISO setting

It might have been simpler to have a single “perceived image quality” metric that could be measured at different ISO levels. This is particularly relevant because some cameras excel in high ISO conditions (requires a low noise floor) while others excel in low ISO conditions (requires physically large sensor). Showing a high-level graph with a single figure of merit per ISO setting might have simplified interpreting the results.

Sensor size visualization

DxOMark’s online graphs allow you to plot scores with MPixels along the horizontal axis. It would be nice to have an extra setting to show sensor size instead of MPixels. This would (just like many of the graphs in this article) cluster comparable products together. Representing sensor size as color would also help because photographers tend to consider different sensor sizes (unlike MPixel ratings) as different product categories.

Summary

• DxOMark Camera Sensor is all about noise.
  DxOMark Camera Sensor measures the noise-related image quality of camera bodies. Resolution and lens sharpness are covered by another DxOMark benchmark.
• Comparing different resolutions
  In order to compare DxOMark Camera Sensor measurements, you need to look at the “Print” mode (aka resolution-normalized) results. These can be directly compared across cameras with different resolutions. The overall DxOMark Sensor score is “Print” level. In the 3 more detailed scores you can choose between “Print” (default) and “Screen”. Just ignore the “Screen” setting.
• Sensor size matters
  Increasing the physical sensor size should reduce noise. Assuming you can continue to work at the same apertures, an N× increase in sensor area should roughly give you an N× higher ISO setting assuming your new lens is just as fast as your old one. The area increase from “Four Thirds” to full-frame is 4×. See Figure 6.
• Large sensors need larger lenses
  If you choose a N× larger sensor area to get lower noise, and you can’t increase your exposure time, you will need a lens with an N× larger area to collect extra light (catch more “photons”). This allows your aperture value to stay the same. And this translates to extra weight, space, and costs. If you leave the lens diameter the same, you will get a smaller f-stop and this will essentially cancel out your larger sensor’s benefit if you shoot at a higher ISO to keep your shutter speeds the same.
• Sensor improvements enable more smaller cameras
  New sensors often outperform older sensors. A new state-of-the-art sensor may allow you to migrate to a smaller camera (for convenience) at the same image quality at the same ISO/f-stop settings. See Figure 2.
  Even without relying on innovation in sensor technology, if you can increase the crop factor by “c”, you will decrease the focal length by c, you should try to decrease the aperture setting by “c” (to achieve the same depth of field) and decrease the ISO setting by “c” (to get the noise down, while utilizing the extra light coming though your faster last). If you manage all this, you will stay on Falk Lumo’s “equivalence” curve. This should produce identical looking images: same field of view, same motion blur, same diffraction, same depth of field and especially same image quality – but using a smaller sensor. Remember that this shrinking trick will even work without having to use a fundamentally better sensor technology.
• Resolution doesn’t increase noise
  Increasing resolution (MPixels) for a given sensor size has no direct impact on image noise. In fact, some of the lowest noise cameras (Nikon D800, Nikon D3x, Pentax K-5, Nikon D7000, Sony Alpha 580) have relatively high resolutions. See Figure 1a.
• Winners and losers
  Various brands (notably Canon and medium-format suppliers) are running behind in terms of noise and dynamic range. Until recently, Forth Thirds suppliers were also running behind (Olympus fixed this in their recent models). Particularly Nikon and various newer or formerly less prominent camera brands that use Sony sensors are taking the lead in terms of image noise and particularly dynamic range. As this comparison is strongly influenced by each brand’s latest models, this situation can conceivably change rapidly (as it did when Nikon overtook Canon in terms of noise performance back in 2007). See Figure 2.
• Definitions
  You can’t directly compare DxOMark’s measurements to numbers from other sources. Each source has a slightly different definition or measurement approach. Example: DxOMark Dynamic Range results are higher than most other sources because of DxOMark’s definition. With a bit of math skills you may be able to convert back and forth using the formulas in this article. But in any case keep in mind that there is no agreed standard across benchmarks. Example: other sources typically don’t normalize noise to a fixed resolution.
• Small sensors are doing surprisingly well
  Very small sensors performed worse than their bigger counterparts. But some of the newer small sensors perform surprisingly wellif you compensate for their area handicap. These models actually outperform all other cameras per unit area.
• Largest sensors disappoint
  At the other end of the scale, the larger-than-full-frame sensors don’t perform as well as they should given their head start over full-frame and APS-C sensors. This suggests there is significant room for improvement there. See Figure 6.

Peter van den Hamer
December 2012

About Peter van den Hamer

Peter van den Hamer is a physicist by training who has been working in the Netherlands as a scientist/architect in various large high-tech and electronics companies for 25 years. Apart from merely writing about technical aspects of photography, he also does some actual photography and has exhibited work at local art galleries. The most recent exhibition at the local town hall ended in the loss of these displayed signed and numbered prints when the building went up in flames in a bizarre [79] incident.

Peter van be reached via his website, viaFacebookorLinkedIn.

Notes

[1]/dxomark-sensor-for-benchmarking-cameras/

[2]Thefirstunwieldy digital camera prototype was built by Kodak in 1975 and Canon’s revolutionarily pricedD30dates back to 2000.

[3] Canon’s full-frame 5D Mark II was state-of-the-art when it was launched in 2008. In early 2012, it was overtaken in both resolution and noise performance by Nikon’s entry-level DLSR (D3200) with a 1.5× crop sensor.

[4] This is the Sony RX100, although Sony doesn’t use the Nikon’s marketing term “CX” sensor.

[5]Starting in 2014, Formula 1 racing is planning to switch to a somewhat more environmentally friendly engine design built around a 1.6 liter turbo engine (http://en.wikipedia.org/wiki/Formula_One_engines).

[6]The Nikon D800 and D600 have higher DxOMark scores than Canon’s competing 5D Mark III and 6D. The Nikon D3200 and D5200 outperform respectively the Canon 650D and (older) 60D. Nikon’s flagship D4 outperforms (somewhat) Canon’s equivalent, the 1Dx. Note that at high ISO, the recent Canon models are actually better than the top-level DxOMark scores suggest. This can be seen by comparing the DxOMark Dynamic Range scores at high ISO settings as shown in Figure 7.

[7] See http://www.chipworks.com/blog/technologyblog/2012/10/24/full-frame-dslr-cameras-canon-stays-the-course/. The essence is that Sony (and thus Nikon) introduced analog-to-digital convertersper ccolumn intheir CMOS sensors a few years ago. It requires a modern chip manufacturing process to fit thousands of column ADCs onto a chip. Sony also stresses its use of patented digital (rather than analog) compensation for dark frame subtraction. This subtraction computes the signal level per pixel relative to the empty/reset level of that pixel and is known as Correlated Double Sampling (in both its analog and digital form). It is unclear whether Sony’s elegant digital CDS technique (http://www.google.com/patents/US7375672) substantially contributes to the excellent performance of current Sony sensors (as suggested by Sony marketing material).

[8]https://en.wikipedia.org/wiki/Silver_Blaze. Inspectory Gregory: “Is there any point to which you would wish to draw my attention?” Sherlock Holmes: “To the curious incident of the dog in the night-time.” “The dog did nothing in the night-time.” “That was the curious incident,” remarked Sherlock Holmes.

[9]This means the benchmark covers the impact of semi-transparent mirrors, anti-aliasing filters, color filter arrays, the sensor itself, signal amplifiers, analog-to-digital convertors, and subsequent signal processing within the camera. Arguably, the decoding of the Raw file is also in scope, but this should have no impact.

[10]https://www.dxo.com

[11]https://www.dxomark.com/index.php/en../About/Company/DxOMark-Conditions-of-Use

[12]https://www.dxomark.com/index.php/Lenses/Camera-Lens-Ratings

[13] The DxOMark Lens score emphasizes resolution, but unlike typical resolution benchmarks, it awards a bonus to wide aperture lenses: these lenses may not be be optimally sharp when used wide open, but by capturing more light at full aperture, they effectively reduce the amount of noise in low light situations.

[14] Given that perceived print quality is a mix of noise and resolution, it may sound tempting to ask that both factors are merged into a single score. DxOMark Sensor score don’t do this. This is presumably because there is no real objective answer possible to the question whether camera/lens combination X or Y produces better image quality.  X may have less noise (which is sometime a problem) while Y may have higher resolution (and thus scale better to larger print sizes).

[15] The answer is “400 ISO”. The short version is that the Four Thirds sensor has ¼ of the surface area compared to a full-frame sensor. So it has the same noise level as a full-frame sensor which is underexposed by 4×. Note that Falk Lumo would likely disagree with the relevance of the question. Instead he would ask “At what aperture and ISO value would a Four Thirds camera produce indistinguishable results to the full-frame / 100 ISO / f/2.8 image?”. See Table 1.

[16]  The repeatability of the score can be estimated by comparing the scores for virtually identical cameras. These pairs of twins include:

• a pre-production Canon 550D has been published along with the actual production model
• the Canon S95 and G12 models (believed to have virtually identical technology in a different housing)
• the Nikon D800 and D800E (in which part of the low pass filter has been rotated to disable anti-aliasing)
• the Pentax K-5 II and K-5 IIs (also with a disabled anti-aliasing filter)

[17] They are called Four Thirds partly because that is their width to height ratio – a ratio that was uncommon for high end cameras. They are also called 4/3 because of a historical naming convention which described sensor sizes in terms of the diameter of glass camera tubes. See http://en.wikipedia.org/wiki/Four_Thirds_system#Sensor_size_and_aspect_ratio.

[18] The scale is a continuous color gradient (Matlab-style colormap). If you want to use the same coloring convention formula to represent sensor size, contact me for help.

[19] Sony calls this “translucent”, but this is technically not a very appropriate term. Frosted glass is translucent. Using the right term keeps Ken Rockwell happy 😉

[20] The semi-transparent mirror gives a handicap of a few points because the mirror diverts some light for the autofocus sensor. This handicap is relatively minor: 70% of the light reaches the sensor. That is equivalent to loosing 0.5 stop of light. 15 points was 1 stop according to DxO, so photographing through Sony’s pellicle mirror (or through a 0.5 EV gray filter) should cost about 8 DxOMark Sensor points. Adding 8 points to the Sony Alpha 55’s score (73) brings the camera on par with the Nikon D7000 (80) and Pentax K-5 (82) and Sony Alpha-580 (80) which are believed to use comparable Sony 16 MPixel sensors  (likely Sony’s IMX071).

[21]Because Canon is the only supplier in the 1.6× APS-C and 1.3× APS-H categories, we can best compare these against e.g. 1.5× APS-C.

[22]Note that this may partly reflect that medium format cameras are designed for high resolution and color rendering: on a tripod, high ISO can often be avoided and in a studio flashes can provide enough light. The dynamic range can be controlled by providing enough lights or reflectors.

[23]5 MPixel for A3 (with a bit of border) corresponds nicely to the 180 DPI lower limit recommended for gallery-quality prints in Luminous Landscape’s inFrom Camera To Print – Fine Art Printing Tutorial.

[24]https://en.wikipedia.org/wiki/Bayer_filter

[25]https://en.wikipedia.org/wiki/Demosaicing

[26]These include some relatively new models that haven’t been tested yet (e.g. Fujifilm’s X-E1), some that might not be mainstream enough to ever get tested (e.g. Leica’s monochrome M8-M) as well as several noteworthy classic models (e.g. Canon Powershot G7).

[27]This scaling is often done automatically when you print or view the results.

[28]As sensor folks say, “they have the same fill factor” or as chip designers say “it’s an optical shrink”. The bowl/cup shapes shown here are horizontally scaled versions of each other, thus leading to identical fill factors.

[29]https://en.wikipedia.org/wiki/Poisson_distribution

[30]If you have the courage to dive deeper, there is a tutorial series atwww.harvestimaging.comthat describes the various sources of sensor noise. It is by Albert Theuwissen, a leading expert on image sensor modeling. I created a synopsis of this 100-page seriesin another posting(http://peter.vdhamer.com/2010/12/25/harvest-imaging-ptc-series/).

[31]When expressed in millimeters, or in water volume per unit of area.

[32]Cups that on average catch λ drops during the exposure to rain will have an expected standard deviation of sqrt(λ) drops. To estimate the rainfall ρ we get ρ = λ × drop_volume / measurement_area. The expected value of ρ is independent of cup size. The variation of ρ decreases when larger cups are used. In Figure 4, ρ would be the depth of the water in the cups if the cups had been simple cylinders. So as λ is increased (bigger cups or longer exposure), the Signal-to-Noise ratio improves. But ultimately we care about how hard it rains, rather than caring about droplets per measuring cup. If you measure rainfall with a ruler to see how deep the puddles are, you will get a result that doesn’t depend on puddle size, and the variations due to droplet statistics will decrease for larger pools of water.

[33]If you still don’t believe this, go read DxO’s white paper “Contrary to conventional wisdom, higher resolution actually compensates for noise”.http://www.dxomark.com/index.php/Publications/DxOMark-Insights/More-pixels-offset-noise!

[34]To make the model more complete, you could:

• Measure the amount of water in the cup by weighing each cup. If you don’t subtract the weight of the empty cup, you have a significant “offset”. If you do subtract the weight of empty cups, the correction will not be perfect.
• Assume some random errors when measuring the amount of water per cup. This “temporal” noise has a fixed standard deviation, and has most impact when the cups are nearly empty.
• Assume that the cups are not perfectly shaped (“Fixed Pattern Noise”). Maybe rows or columns of cups came from the same batch and have correlating manufacturing deviations (“row or column Fixed Pattern Noise”).
• Drill a hole near the top of each cup so that excess water from one cup doesn’t overflow into neighboring cups. The holes will have slight variations in their location or size: “saturation or anti-blooming non-uniformity”.
• Place the cups in a tray of water. If the cups are slightly leaky (unglazed flower pots), you will get some water leaking in from the surroundings into the cups (“dark current or dark signal”). Not all cups will leak equally fast (“dark signal non-uniformity”). And at higher temperatures, you will see a bit faster leakage (it would be too tricky to emulate the exponential temperature dependency without some really fancy materials).
• Break a few cups or their measurement scales (“defective pixels”).

The above covers all the noise sources in the PTC tutorial onwww.harvestimaging.com.

[35]For info on the value of λ or “the full well capacity”, see Roger Clarke’s website. Seehttps://www.clarkvision.com/articles/digital.sensor.performance.summary/#full_well. More recent data derived by “curve fitting” the DxOMark measurements can be found athttp://www.sensorgen.info/.

[36]DxOMark’s value for the signal to noise ratio (SNR) of the Nikon D800 at 100 ISO near saturation can be found athttps://www.dxomark.com/index.php/Cameras/Camera-Sensor-Database/Nikon/D800by selecting the “Measurements” tab and then “Full SNR”. At 100% gray, 100 ISO gives 43.3 dB. This is lower than the expected 46 dB due to curvature in the graph at high light intensities (likely anti-blooming or controlled overflow circuitry): extrapolation of the 100 ISO line between 0.2% gray and 10% gray results in an estimate of 46.7 dB. The latter value would correspond to λ=46,777 electrons, which is in line withwww.sensorgen.info‘s fit of λ=44,972 electrons.

[37]You would get the same statistics when you measure rain using2 literpans. Two liters correspond to about 40,000 drops of water.

[38]The actual DxOMark measurement value at 6% gray and 100 ISO is 34.4 dB.

[39]The only way to improve this signal-to-noise ratio is to increase the value of λ. A drastic 4x decrease in the number of MPixels would boost λ by 4× and increase the signal to noise ratio by 2× (square root of λ). We will see later that the impact of decreasing the number of MPixels is cancelled out by scaling statistics.

[40]The only variable you can control is the full-well capacity per unit area (bucket depth), but this number does not vary dramatically. Example: the Canon 5D2 and the 5D3 only differ by 5%. When you compensate for the difference in resolution, this is still only a 15% change in 3.5 years time.

[41]See endnote 25.

[42]Or, for that matter, for any other way to view an image in its entirety without zooming in and out all the time.

[43]Some cameras like the Canon 5D Mark II do this digitally. Canon calls these Raw modes SRaw and they have unusual MPixel ratios like 5.2 to 10.0 to 21.0.

[44]Note that although this scaling story holds for photon shot noise and dark current shot noise, other noise sources don’t necessarily scale the same way. In particular, some very high-end CCDs can use a special analog trick (“charge binning”) to sum the pixels, thus reducing the amount of times that a readout is required. This would reduce temporal noise by a further sqrt(N) where N is the number of pixels that are binned. Apart from the fact that only exotic sensors have this capability (Phase One’s Pixel+ technology), DxOMark’s data suggest that this extra improvement doesn’t play a significant role.

[45]/reviews/cameras/sensor-plus-review/

[46]https://image-sensors-world.blogspot.nl/2012/10/chipworks-reviews-full-frame-dslr.html

[47]This is due to a combination of lens quality and optical diffraction. For info on diffraction:https://www.cambridgeincolour.com/tutorials/diffraction-photography.htm

[48]Maintaining the same aperture in order to keep the same exposure time implicitly assumes that one wants to maintain the same (e.g. “base”) ISO setting. As a side effect, this lowers the depth of field and lowers the noise level on larger sensors. This is often considered desirable. But as pointed out by Falk Lumo (discussed in the next section) this is only one option.

[49]https://www.falklumo.com/lumolabs/articles/equivalence/: Camera Equivalence by Falk Lumo

[50]For simplicity we assume the sensors all have the same aspect ratio or that differences in aspect ratio are cropped away in the resulting image.

[51]https://www.dxomark.com/index.php/About/Sensor-scores/Use-Case-Scores

[52]The measured values are at the lowest measured (rather than nominal) ISO setting. The camera with the lowest measured ISO setting has a slight advantage that disappears at higher ISO settings like 200 ISO. See Measurements | Dynamic Range tab for the graphs onwww.DxOMark.com.

[53]I do not shoot weddings. As I was nevertheless requested to shoot a close friend’s indoor wedding, I rented a Canon 5D3 with some fast lenses (e.g. 24 mm/1.4 II and 85 mm/1.2) – just to be on the safe side.

[54]Actually Lightroom shows that some spots are overexposed. This could easily be fixed with the LR4 highlights slider, but I prefer to shown the unprocessed photo.

[55](0.05/90)^(1/2.2)=3.3% on Lightroom’s histogram readout whereby 2.2 is the presumed gamma value.

[56]For a presentation by Hugo Gaggioni, the CTO of Sony’s Broadcast and Production Systems division on this go to http://pro.sony.com/bbsc/video/videoChannelSearchResults.do?pageno=2&navId=4294963750&sort=relevance&srchTerm=sensor&pagerecs=12&view=grid and click on the “CCD & CMOS” thumbnail. Sony’s Exmor technology is discussed between 22:00 and 29:47.

[57]The use of on-chip or per-column ADCs has multiple benefits. Firstly, the analog signals are measured closer to the source, thus reducing the chance of interference (EMI) associated with long wires and small signals. Secondly, the rate at which column ADCs measure pixels is reduced by roughly 1000x (image width in pixels divided by number of sampling channels). This means that the ADC can take e.g. 1000 times longer to measure each individual pixel. As mentioned inhttp://en.wikipedia.org/wiki/Analog-to-digital_converter, “There is, as expected, somewhat of a tradeoff between speed and precision.” So a radical reduction in the speed requirement can be expected to improve precision and thus noise.

[58]http://en.wikipedia.org/wiki/Tare_weight

[59]http://www.chipworks.com/blog/technologyblog/2012/10/24/full-frame-dslr-cameras-canon-stays-the-course/

[60]The CMOS chip is made of silicon, but the wiring is done using copper instead of aluminum. Sony already uses this technology.

[61]0 dB doesn’t mean zero signal. It means signal and noise are equally strong.

[62]Ln(sqrt(16 MPixels/8 MPixels))/Ln(2) = 0.5 EV. There are smarter ways to calculate this, but this works.

[63]Choosing a reference resolution of 16 MPixels instead of 8 MPixels would thus decrease all the DxOMark Print mode dynamic range numbers by 0.5 EV.

[64]The benchmark doesn’t depend on the actual steps (e.g. 1.0 stop or 1/3 stop) in which a user can adjust the ISO setting. Results for intermediate values are generated by interpolation.

[65]Strictly speaking, the definition doesn’t allow you to express the Low-Light ISO behavior of a camera with a small enough sensor if the camera fails to meet one or more of the three criteria at its base ISO setting. But one of the tested models (Panasonic DMC FZ28) actually has a Low-Light ISO rating that falls below the (both nominal and actual) ISO range of the camera. So apparently this benchmark accepts extrapolated results.

[66]Pruning down the sensor would reduce the resolution. But until the pixels get very small, the DxOMark results should be roughly independent of resolution.

[67]Creating an array of about 30 tiled Q sensors would result in a full-frame sensor which, in theory, would outperform the reigning Nikon D3s! And – assuming one could do the tiling seamlessly and could handle all the resulting data – would result in a 360 MPixelübersensor. Or you could make a 700 MPixel medium-format sensor that would outperform all full-frame and medium-format sensors. Actually this may put Canon’s 120 MPixel “proof-of-concept” APS-H sensor (August 24th 2010) into perspective: when scaled from APS-H to full-frame, the Pentax Q technology would give 200 MPixels. I don’t know what the purpose of Canon’s proof-of-concept sensors was: convince Canon management about scaling laws, test a manufacturing technology or test the waters for niche applications?

[68]The value we get here should be equal or greater to the value provided by DxOMark: we are only checking one of the three rules here.

[69]Often the actual sensitivity is lower than expected (by e.g. almost 1 stop on the PEN E-PL5). This helps the camera look better in benchmarks.

[70]See the Measurements à Color Response tab → Sensitivity metamerism index, ISO 17321. Because SMI is ignored in the DxOMark Camera Sensor score, is unrelated to noise, and is really hard to explain we won’t discuss it here.

[71]http://www.dxomark.com/index.php/Publications/DxOMark-Insights/Canon-500D-T1i-vs.-Nikon-D5000

[72]In particular, DxOMark’s analysis is that Color Filter Array colors that have too much overlap in their transmission spectra increase chroma noise. Too little overlap decreases chroma noise at the cost of more luminance noise. This is an example how the details of a benchmark can impact design choices.

[73]It doesn’t mean that each channel is sampled at 8 bit: each channel is typically sampled at 12-16 bit. The actual formulas for Color Depth reflect the amount of noise in each channel and are too complex to explain here (integrals).

[74]Although I have a science and semiconductor industry background, I am not an image quality expert.

[75]Both Dynamic Range and Color Sensitivity are measured at low ISO. This possibly gives a 2:1 bias towards the low ISO side and stresses differences there that may not be normally visible. As illustrated in Figure 7, top notch low ISO performance is no guarantee for top notch high ISO performance.

[76]For details and references, see sections on Falk Lumo’s Equivalence Theorem above.

[77]There are more aspects than Depth of Field, but this is the easiest one.

[78]Expressed in a linear formula: DxOMark_Sensor_Score = 59 + 4.3*(ColorDepth-21.1) + 3.4*(DynamicRange-11.3) + 4.4*log2(ISO/663) -0.2. The 3 middle terms can either add or subtract points, depending on whether the camera did better or worse than the Leica M8. Expansion of the formula gets rid of the choice of the Leica M8 as a reference. Camera scores predicted by this formula differ from the published DxOMark Sensor scores by a standard deviation of 0.7. The formula tells us that the 3 subbenchmarks have roughly equal importance. And that a factor of 2 improvement in each subbenchmark would increase the overall score by 12.1 points. My guess is that the actual formula is non-linear and may use (under some conditions) coefficients of 5/5/5 rather than 4.3/3.4/4.4.

[79]http://www.dutchnews.nl/news/archives/2012/07/town_hall_destroyed_by_fire_af.php

Elevate Your Vision

Join our community of passionate photographers.

Access our extensive knowledge archive.

Master the art of landscape and beyond.

Your Email *

Select list(s) to subscribe to

Constant Contact Use. Please leave this field blank.

By subscribing I agree with Terms and Conditions

Do it later